里德伯常数

---

简介

瑞典物理学家约翰内斯·里德伯引入里德伯公式，该公式代表原子物理学的基态常数。它描述了不同系列中光的频率或波长，这与谱线有关。它尤其强调了氢原子从巴尔末系发射的光。该常数的标准通常基于一个前提。原子的原子核通常发射的光与单个轨道电子相比极其巨大。里德伯常数的特定值为每米 10,973,731.56816。

里德伯常数及其解释

里德伯公式是指用于预测由在特定原子能级之间移动的电子产生的光的波长的数学公式。电子在从一个轨道到另一个轨道移动过程中，其能量发生变化 (Stávek, 2021)。当某个电子将其当前轨道从高能态变为低能态时，就会产生光子。同样，当电子从高能态移动到低能态时，通常会观察到原子发出的光子。

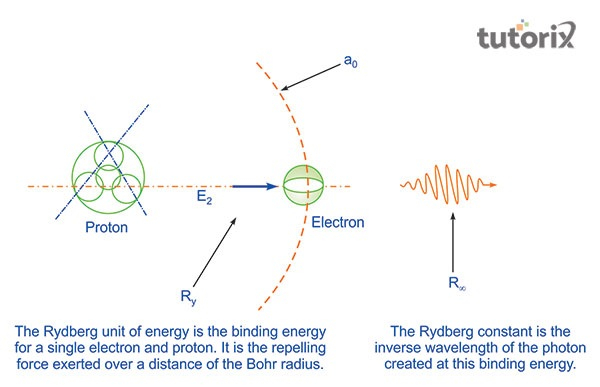
图1：里德伯单位能量和里德伯常数

每个成分都具有不同的光谱指纹。当特定元素的气态被加热时，它会发出光。当光穿过特定的棱镜时，会注意到不同颜色的亮线 (Beyer *et al.*, 2017)。每个成分都略有不同 (Yarman *et al.*, 2018)。这一利用是名为光谱学的学科研究的开端。R_H 或 R_∞ 表示里德伯常数，它是与每种元素的原子光谱相关的波数。

里德伯常数及其意义

在原子物理学领域，里德伯常数具有重要意义。它与基本原子常数 e、h、c 和 m_e 相关。巴尔末系的原子系列可以用这个方程来解释。

$$n = \frac{n_0 - N_0}{m + m'}$$

$$n = n_0 - N_0/(m + m')$$

其中，

M = 自然数

M' 和 n₀ = 特定系列的量子亏损

n₀ = 里德伯常数

里德伯常数通常用作能量单位。

光速

光速可以通过各种材料传播。光的特定速度测量值为 3 * 10⁸ 米/秒。光速是自然界中不可或缺的概念。关于光速，E=mc² 是测量光速的重要因素。关于里德伯常数 (R)，表示为 R_hc，这里，h 表示普朗克常数，c 表示光速 (Suto, 2021)。R_hc 的量纲公式与能量的量纲公式相同。

里德伯常数：量纲公式

里德伯常数的量纲公式可以描述为解释由在原子内移动能级的特定电子发射的光的波长的数学公式 (Ramos, Moore & Raithel, 2017)。公式如下：

$$ \frac{1}{\lambda} = RZ^2(\frac{1}{n_1^2} - \frac{1}{n_2^2}) $$

这里，

Z = 原子的原子序数

n₂ 和 n₁ 是整数，这里 n₂ > n₁。随后，据说 n₁ 和 n₂ 与能量量子数相关。

里德伯常数的推导

在经典方法中，里德伯常数来自精细结构常数和电子半径。里德伯常数特别是波的形式，它来自波长方程。波的形式基于 K = 10（即 10 个波中心）。这用于计算氢。考虑氢光谱，其中原子具有能量 E，这表示动能 (k) 的总和，P 是移动电子的能量。

$$ E = K + P $$

$$ K = \frac{1}{2 \times m_{电子} \times u^2} $$

$$ P = \frac{q_1 \times q_2}{4\pi \epsilon_0 r} \epsilon_0 = 空间介电常数 $$

$$ = \frac{Ze \times (-e)}{4\pi \epsilon_0 r} Z 是质子的数量 $$

$$ = -\frac{Ze^2}{4\pi \epsilon_0 r} $$

氢原子的里德伯常数

每个原子都可能发射大量磁辐射。原子发射的磁辐射对该特定原子是唯一的。

图3：氢原子：线光谱

上图突出显示氢原子在可见光区域内发射四种不同类型的波长，分别为 410 nm、434 nm、486 nm 和 656 nm。光的波长向下方向增加。根据 Shaffer (2020) 的说法，原子光谱的离散线决定了构成它的光波长。在氢原子的特定情况下，它在可见光区域内形成遵循特定模式的离散线。氢原子线光谱之间的间距以规则间隔减小，被称为**氢原子的巴尔末系**。然而，1885 年，巴尔末表明，可见光区域内的氢光谱具有特定遵循里德伯方程的波长。

图4：当 H 原子转移到另一个能级时波长的发射

$\frac{1}{\lambda} = R[\frac{1}{2^2} - \frac{1}{n^2}]$ n 是主量子数。$R = 1.09677576 \times 10^7 m^{-1}$ 假设当氢原子从 n=4 能级转移到 n=2 能级时，H 原子发射的光的波长为 $\frac{1}{\lambda} = R[\frac{1}{2^2} - \frac{1}{n^2}]$

$\frac{1}{\lambda} = 1.09677576 \times 10^7 [\frac{1}{4} - \frac{1}{16}]$

$\lambda = 486 nm$

总结

在光谱学领域，里德伯常数是指特定原子的电磁光谱。由于它可以被精确测定，因此它一直是原子物理学的基本常数之一，因为它与基本原子常数 (h、e、c、m_e) 建立了联系。

常见问题

Q1. R_∞ 和 R_H 代表什么？

A. R_∞ 指的是高原子，R_H 指的是氢。它与里德伯常数相关。它是里德伯常数的一部分。

Q2. 里德伯常数的重要性是什么？

A. 里德伯常数在原子物理学领域具有重要意义。它与原子物理学基本常数的概念相关。

Q3. 里德伯常数的值基于什么因素？

A. 里德伯常数的值基于一个特定事实，该事实表明特定原子发射光的原子核比单个轨道电子大得多。

Q4. 什么是巴尔末系？

A. 原子物理学的巴尔末系是指一组 6 个命名系列，用于描述氢原子的谱线发射。巴尔末公式用于计算巴尔末系。