SVM中的分离平面

---

支持向量机 (SVM) 是一种广泛应用于手写识别、情感分析等领域的监督学习算法。为了分离不同的类别，SVM 计算最优超平面，该超平面或多或少准确地在两个类别之间创建了一个边界。

以下是一些在 SVM 中分离超平面的方法。

• 数据预处理 - SVM 需要经过标准化、缩放和中心化处理的数据，因为它们对这些特征敏感。

• 选择核函数 - 核函数用于将输入转换为更高维的空间。其中一些包括线性核、多项式核和径向基函数。

让我们考虑 SVM 超平面可以区分的两种情况。

• 线性可分情况。

• 非线性可分情况。

示例 1

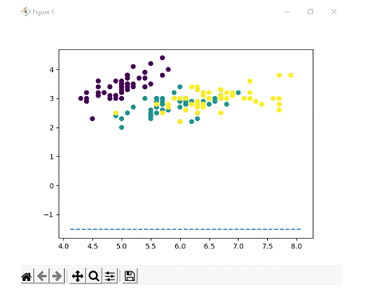
对于线性可分情况，让我们考虑具有二维特征的鸢尾花数据集。线性可分情况是指特征可以通过超平面线性分离。鸢尾花数据集是展示线性可分超平面的一个很好的初学者友好方法。目标是显示一个本质上是线性的超平面。

算法

• 导入所有库

• 加载鸢尾花数据集，并将数据和目标特征分别分配给变量 x 和 y。

• 使用 train_test_split 函数，为 x_train、x_test、y_train 和 y_test 分配值。

• 使用线性核构建 SVM 模型，并根据训练数据点拟合模型。

• 预测标签并打印模型的准确率。

• 使用模型将模型的权重和偏置分别作为模型的系数和直线的截距。

• 使用权重和偏置计算斜率和 y 截距。

• 在图表中绘制数据点并展示它。

from sklearn import datasets
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split as tts
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt
import numpy as np

iris=datasets.load_iris()
x=iris.data
y=iris.target

x_train, x_test, y_train, y_test = tts(x,y,test_size=0.3,random_state=10)

#build an SVM model with linear kernel
clf=SVC(kernel='linear')

#fit the model
clf.fit(x_train,y_train)

#predict the labels
y_pred=clf.predict(x_test)

#calculate the accuracy
acc=accuracy_score(y_test,y_pred)
print("Accuracy: ", acc)

#get the hyperplane parameters
w=clf.coef_[0]
b=clf.intercept_[0]

#calculate the slope and intercept
slope = -w[0]/w[1]
y_int = -b/w[1]

#plot the dataset and hyperplane
plt.scatter(x[:,0], x[:,1], c=y)
axes=plt.gca()
x_vals=np.array(axes.get_xlim())
y_vals=y_int+slope*x_vals
plt.plot(x_vals, y_vals, '--')
plt.show()

我们将数据集分成训练集和测试集，其中测试集占总数据的 30%。然后，我们创建一个具有线性核的 SVM 分类器，并将模型拟合到训练数据。

我们预测测试数据的标签，并将获得的结果存储在单独的变量中，通过将预测值与真实值进行比较来计算模型的准确率，并打印获得的准确率，即 1.0。

然后从训练数据集检索超平面的参数，并计算超平面的斜率和截距，然后使用散点图绘制，每个类别使用不同的颜色。

Accuracy: 1.0

输出

示例 2

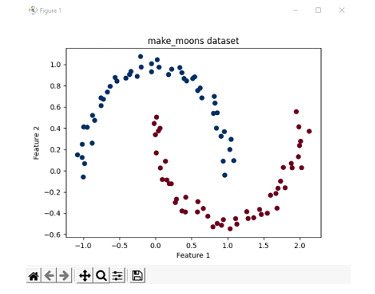
考虑一个案例不线性可分的情况。在这种情况下，我们使用 scikit-learn 库中提供的 make_moons 数据集。make_moons 数据集是展示 2 个或多个类别不线性可分情况的好方法。因此，此示例用于描述非线性可分情况。

让我们首先打印数据集的数据点，以便了解我们正在处理什么。

算法

• 导入所有必要的库。

• 使用 100 个样本生成 make_moons 数据集，并具有最小的噪声水平。

• 在图表中绘制这些数据点并打印，并将颜色图设置为红色和蓝色。

import matplotlib.pyplot as plt
from sklearn.datasets import make_moons

# Generate the make_moons dataset with 100 samples and a noise level of 0.05
X, y = make_moons(n_samples=100, noise=0.05, random_state=42)

# To show the dataset
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.RdBu_r)

# Set the plot labels and title
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('make_moons dataset')

# Show the plot
plt.show()

输出

算法

• 导入程序中使用的所有库

• 从 make_moons 数据集中生成 100 个数据样本，噪声尽可能低。

• 使用径向基函数 (RBF) 核初始化 SVC 分类器，并根据分类器训练数据点。

• 根据数据点，将前面初始化的分类器拟合到数据集。

• 查找数据中特征和标签的最大值和最小值。

• 使用上述值，使用 linspace 函数构造网格。

• 要返回网格的一维表示，应用 ravel 函数并使用 np.c_ 沿第二轴切片。

• 要定义决策边界，创建决策边界的等高线图。

• 打印图像和标签。

示例

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.svm import SVC

# load moons dataset
x, y = datasets.make_moons(n_samples=100, noise=0.15, random_state=42)

# create an SVM classifier implementing RBF kernel
clf = SVC(kernel='rbf', gamma=2)

# train the classifier on the dataset
clf.fit(X, y)

# create a meshgrid representing features and labels
x_min, x_max = x[:, 0].min() - 0.1, x[:, 0].max() + 0.1
y_min, y_max = x[:, 1].min() - 0.1, x[:, 1].max() + 0.1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 500), np.linspace(y_min, y_max, 500))
z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
z = z.reshape(xx.shape)

# create a contour plot of the decision boundary
plt.contourf(xx, yy, z, cmap=plt.cm.RdBu, alpha=0.8)
plt.scatter(x[:, 0], x[:, 1], c=y, cmap=plt.cm.RdBu_r)

# set the plot labels and title
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('SVM Decision Boundary')

# show the plot
plt.show()

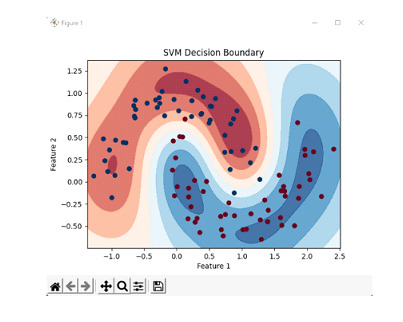
我们通过创建 100 个样本（噪声级别为 0.15，随机种子为 42）生成数据集，并创建一个 SVM 分类器，并在数据集上训练分类器。然后，我们定义一组点来表示特征和标签。然后，我们计算这些点的决策函数值，并将其重新整形以匹配网格的维度。然后，我们创建决策边界的等高线图，其中决策函数值决定区域的颜色。我们还绘制原始数据点，不同颜色代表不同类别。

输出

结论

支持向量机是更广泛使用的算法之一，用于各种领域，主要是文本和语音分类，或 NLP 中的情感分析。它在分类方面的多功能性使其成为更受欢迎的算法之一。

在其他情况下，它有其自身的缺点。有时，SVM 在计算上可能非常密集，并且由于模型的敏感性，需要仔细检查提供给模型的数据。