某地一个购物中心30家商店的年度利润构成如下分布
| 利润(以万卢比计) | 商店数量(频数) |
|---|---|
| 大于或等于5 | 30 |
| 大于或等于10 | 28 |
| 大于或等于15 | 16 |
| 大于或等于20 | 14 |
| 大于或等于25 | 10 |
| 大于或等于30 | 7 |
| 大于或等于35 | 3 |
已知
某地一个购物中心30家商店的年度利润构成
如下分布。
要求
我们必须绘制上述数据的两条累积频数曲线,并由此求出中位数。
解答
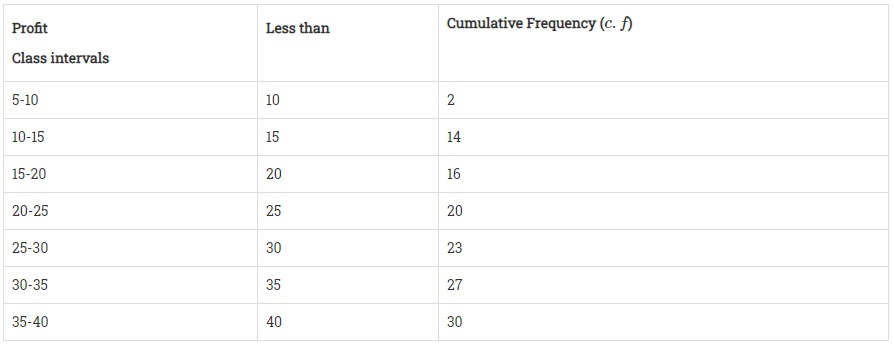
我们首先根据下表准备“大于”方法的累积频数分布表:
| 利润(以万卢比计) | 商店数量 (累积频数) |
| 大于或等于5 | 30 |
| 大于或等于10 | 28 |
| 大于或等于15 | 16 |
| 大于或等于20 | 14 |
| 大于或等于25 | 10 |
| 大于或等于30 | 7 |
| 大于或等于35 | 3 |
将利润(以万卢比计)表示在X轴上,将累积频数表示在Y轴上。
在图上绘制点 (5, 30), (10, 28), (15, 16), (20, 14), (25, 10), (30, 7) 和 (35, 3),并用自由手绘线连接这些点,得到“大于”累积频数曲线。
我们首先根据下表准备“小于”方法的累积频数分布表
将利润(以万卢比计)表示在X轴上,将累积频数表示在Y轴上。
在图上绘制点 (10, 3), (15, 7), (20, 10), (25, 14), (30, 16), (35, 28) 和 (40, 30),并用自由手绘线连接这些点,得到“小于”累积频数曲线。
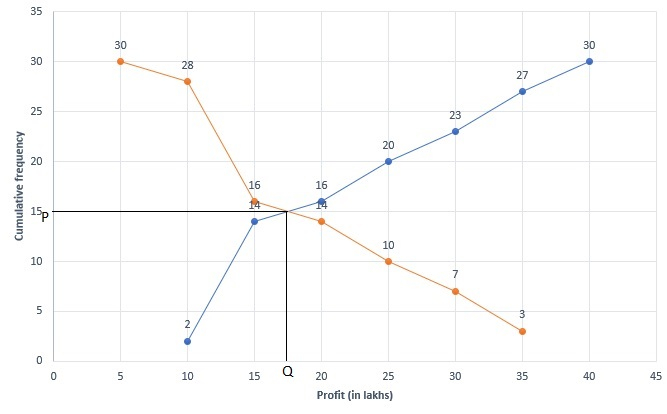
总天数 $N = 30$
这意味着:
$\frac{N}{2} = \frac{30}{2}=15$
在两条累积频数曲线交点处画一条平行于X轴的线,该线进一步与Y轴上的(0, 12)点相交。
在两条累积频数曲线交点处画一条垂直于X轴的线,该线进一步与X轴上的(17.50, 0)点相交。
因此,使用累积频数曲线得到的所需中位数为17.50。
因此,中位数为17.50万卢比。

广告

 数据结构
数据结构 网络
网络 关系型数据库管理系统 (RDBMS)
关系型数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C语言编程
C语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP