一辆汽车的速度-时间图如图 8.12 所示。

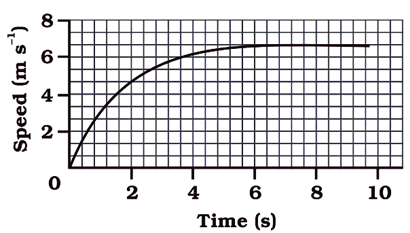
图 8.12
(a). 求出这辆汽车在最初 4 秒内行驶了多远。在图上阴影区域表示汽车在此期间行驶的距离。
(b). 图的哪个部分表示汽车的匀速运动？

(a) 在速度-时间图中

距离 = v-t 图的面积。

这里，我们使用三角形的面积（天蓝色阴影区域）来找到近似面积。

距离 = △OAB 的面积

= $\frac{1}{2}\times b\times h$，其中 b = 底，h = 高

= $\frac{1}{2}\times 4\times 6$ $[\because b=时间,\ h=速度]$

= $12m$

我们仍然没有得到总面积，因为黄色阴影部分没有计算在内。所以，这不是精确的。

因此，为了找到黄色区域和天蓝色区域的面积，我们需要通过计算方格来找到面积。

从图中可以看出：

水平轴上的方格数 (时间轴)

5 个方格 = 2 个单位。

$1\ 个方格=\frac{2}{5}个单位$

垂直轴上的方格数 (速度轴)

3 个方格 = 2 个单位。

$1\ 个方格=\frac{2}{3}个单位$

$\therefore 每个方格的面积=\frac{2}{5}\times \frac{2}{3}\Leftrightarrow \frac{4}{15}平方单位$

所以，1 个方格代表 $\frac{4}{15}m$ 距离。

现在，我们取

$\therefore 总面积=15.2+0.8+0.4+0\Leftrightarrow 16.4平方单位$

因此，汽车在 0-4 秒内行驶的距离 = 16.4m

(b) 时间为 t = 6 s 到 10 s 之间绿色部分的图表示汽车的匀速运动，因为在此时间段内，汽车的速度保持恒定。

教程点

更新于：2022年10月10日

177 次查看

完成课程获得认证

开始

一辆汽车的速度-时间图如图 8.12 所示。图 8.12(a). 求出这辆汽车在最初 4 秒内行驶了多远。在图上阴影区域表示汽车在此期间行驶的距离。(b). 图的哪个部分表示汽车的匀速运动？