使用球面测微计测定给定球面曲率半径

---

半径是圆的特定运动点，它随着运动曲线的变化而自身改变位置。曲率半径是根据曲线位置确定位置的曲线。曲率半径是特定透镜弯曲部分的形成，其中半径是由圆的运动形成的。在本教程中，将重点介绍使用球面测微计计算曲率半径的方法，该方法有助于测量三角形框架。

球面测微计的描述

一种帮助测量三个构成三角形的支脚的仪器，其公式是估计曲率半径的最终过程。三个部分的尖端构成一个等边三角形，并位于圆的半径上。

球面测微计最令人兴奋的特点是，中心部分可以在垂直方向上移动，这有助于对曲率半径进行适当的计算。一个圆形桌面固定在头部，并包含一个刻度，标记边缘的外侧部分。所有不同的部分（球面测微计的支脚）都是可调节的，高度是可读的（Definitions，2022）。此外，球面测微计进行一次旋转相当于 1mn。

图 1：球面测微计

曲率半径公式

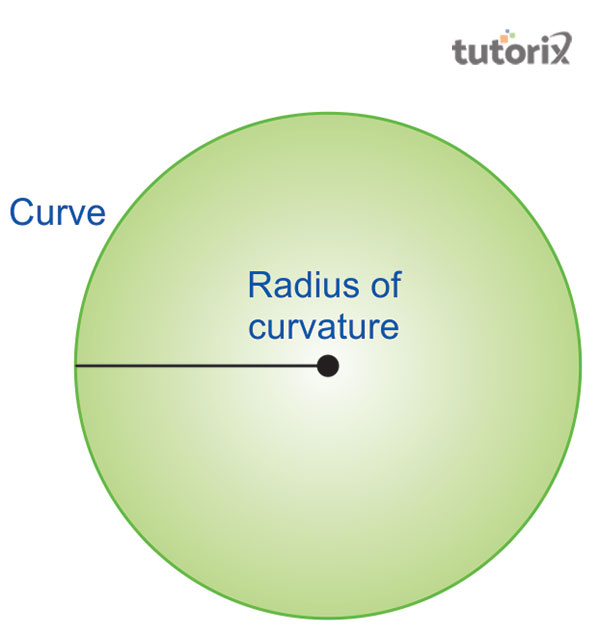
图 2：曲率半径

曲线的曲率半径是在给定特定位置处的圆的半径。圆的运动可能会由于移动圆的半径发生变化而导致曲率发生变化 (Lodder，2018)。

字符“R”表示用于估计曲率半径值的公式。曲线的导数量对曲线是平坦的，它可以用标量量在后面形成曲线 (Sciencing，2022)。

此外，曲率半径是一个虚构的圆，而不是实际的形状或图像。曲率半径是从顶点到曲率中心的长度。“Y”或曲线等于 f(x)，其中“x”表示半径。

主焦点和焦距

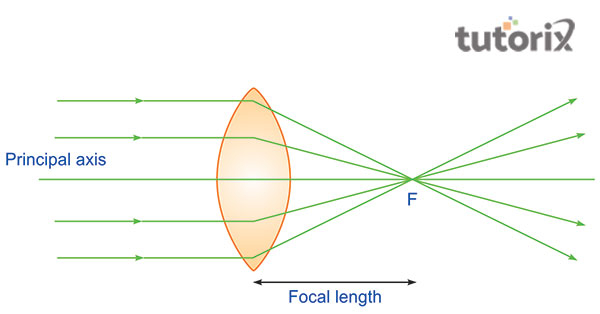
图 3：曲率半径中的主焦点和焦距

当光线从主轴平行于凸透镜通过时，会汇聚到主轴上。由于透镜的汇聚，来自不同方向的光线的交汇点为主焦点，光线在汇聚后到交汇点所经过的区域为焦距 (f) (Chen 等人，2020)。

此外，主焦点和光心之间的距离为焦距，等于曲率半径 R 的一半。

计算步骤

以下步骤是利用球面测微计估计曲率半径计算的实际过程。

• 为了获得速度计的三个孔，学生需要通过抬起中心部分的螺钉并将出现的孔分别标记为 A、B 和 C，将球面测微计推到实践练习本上。
• 在下一步中，学生需要连接练习本上绘制的三个点并形成一个三角形，这有助于更准确地测量这三个孔之间的距离。
• 在下一阶段，学生可以借助点之间距离 AB、BC 和 CA 记录三个平均值。在此步骤之后，记录所用球面测微计的最小刻度和螺距至关重要 (Khakimzyanov & Rashidov，2022)。轻轻向上抬起螺钉是计算过程中的下一步。
• 在下一阶段，学生需要将球面测微计放置在凸透镜表面上，使仪器的三个支脚位于其上。
• 抬起后，学生需要向下旋转螺钉，直到它连接到凸透镜的表面。任何人都可以轻松地记下从圆形刻度上读取的值。
• 在下一阶段，需要取下球面测微计并将其放置在镜子上。学生应记下旋转次数，标记为 n1。
• 此外，在下一步中，使用垂直刻度读取刻度上的值至关重要 (Bergman，2018)。学生需要重复此过程以获得适当的观察结果，直到旋转完成。

序号	圆形（圆盘）刻度读数		平面镜上完全旋转的次数 (n1)	不完全旋转中圆盘刻度分度的数量 x = (a-B)	总读数 h=n1xp+x(L.C) (mn)
1					h1=
2					h2=
3					h3=

结论

本教程旨在借助金属三角形计算曲率半径。球面测微计根据千分尺的原理来计算曲率半径。使用球面测微计设备计算曲率半径的学生需要采取一些额外的预防措施，以避免不必要的误差。凸面是最常用于计算曲率半径的材料。学生需要采取预防措施，例如反复沿同一方向移动螺钉，以避免任何错误或积压。

常见问题

Q1. 曲率半径的公式是什么？

用于计算曲率半径的常用方程是 y=f(x)。曲率半径参数可以帮助测量矢量的长度。

Q2. 在平面表面上，P 和 R 的意义是什么？

“P”和“R”都用于借助凸透镜计算曲率半径。在计算半径的上下文中，P = 0 且 R = 无穷大。

Q3. 速度计的螺距是什么意思？

速度计的螺距是直线螺纹之间的距离，其中螺钉以与旋转轴相同的对齐方式设置。