直流电机中的转矩 - 电枢转矩和轴转矩

转矩定义为力绕轴的转动矩。它由力 (F) 和力作用线到旋转轴的垂直距离 (r) 的乘积来衡量，即

$$\mathrm{转矩,\: 𝜏 = 𝐹 × 𝑟 \:… (1)}$$

转矩的单位是牛顿米 (Nm)。

直流电机的电枢转矩

在直流电机中，在距离 r（电枢半径）处作用于每个导体的周向力 (F) 促使电枢旋转。所有电枢导体转矩之和称为电枢转矩 (τ_a)。

令：

$$\mathrm{𝑃 = 极数}$$

$$\mathrm{𝑟 = 电枢半径}$$

$$\mathrm{𝑙 = 各导体的有效长度}$$

$$\mathrm{𝑍 = 电枢导体总数}$$

$$\mathrm{𝐴 = 并联支路数}$$

$$\mathrm{𝑖 = 各导体中的电流}$$

$$\mathrm{𝐵 = 磁通密度}$$

$$\mathrm{\varphi = 每极磁通}$$

因此，

$$\mathrm{作用于每个导体的力, \:𝐹 = 𝐵 \:𝑖 \:𝑙}$$

$$\mathrm{一个导体产生的转矩 = 𝐹 \times 𝑟}$$

$$\mathrm{\therefore \:总电枢转矩,\: \tau_{𝑎} = 𝑍 × (𝐹 \times 𝑟) = 𝑍 𝐵 𝑖 𝑙 𝑟}$$

由于，

$$\mathrm{各导体中的电流,\: 𝑖 =\frac{𝐼_{𝑎}}{𝐴}}$$

$$\mathrm{磁通密度,\:𝐵 =\frac{\varphi}{𝑎}}$$

其中，

$$\mathrm{𝑎 = 磁通路径在半径 r 处的横截面积 =\frac{2\pi 𝑟𝑙}{𝑃}}$$

$$\mathrm{\therefore \tau_{𝑎} = 𝑍 \times\frac{\varphi}{𝑎}\times\frac{𝐼_{𝑎}}{𝐴}\times 𝑙 \times 𝑟 = 𝑍 \times \frac{\varphi}{2𝜋𝑟𝑙⁄𝑃}\times\frac{𝐼_{𝑎}}{𝐴}\times 𝑙 \times 𝑟}$$

$$\mathrm{⇒ \tau_{𝑎} =\frac{𝑃𝑍}{2\pi 𝐴}\varphi 𝐼_{𝑎} Nm \:… (2)}$$

公式 (2) 中的表达式称为直流电机的电枢转矩。

对于给定的直流电机，(PZ/2πA) 是一个常数。因此，

$$\mathrm{\tau_{𝑎} \varpropto \varphi 𝐼_{𝑎}… (3)}$$

因此，直流电机产生的电枢转矩与每极磁通和电枢电流成正比。

此外，直流电机的反电动势由下式给出：

$$\mathrm{𝐸_{𝑏} =\frac{𝑁𝑃 \varphi 𝑍}{60𝐴}}$$

$$\mathrm{⇒\frac{𝑃\varphi 𝑍}{𝐴}=\frac{60 × 𝐸_{𝑏}}{𝑁}… (4)}$$

由公式 (2) 和 (4)，我们得到：

$$\mathrm{\tau_{𝑎} =\frac{1}{2𝜋}\times (\frac{60 × 𝐸_{𝑏}}{𝑁}) \times 𝐼_{𝑎}}$$

$$\mathrm{⇒ \tau_{𝑎} = 9.55 ×\frac{𝐸_𝑏𝐼_𝑎}{𝑁}Nm\: … (5)}$$

直流电机的轴转矩

直流电机中可用于做有用功的转矩称为轴转矩 (&tau_sh)。

在直流电机中，电机电枢中产生的总转矩并非全部传递到电机轴上，因为一部分转矩损失在克服机器的机械损耗。因此，轴转矩略小于电枢转矩。

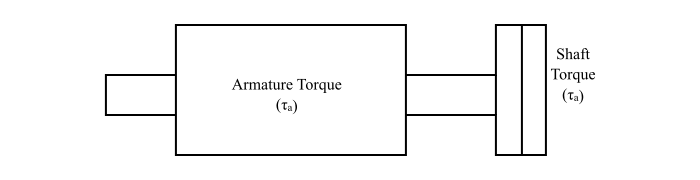
如果电机的转速为 N rpm，则直流电机的输出轴功率（以瓦特为单位）由下式给出：

$$\mathrm{𝑃_{𝑠ℎ} =\frac{2\pi 𝑁\tau_{𝑠ℎ}}{60}}$$

$$\mathrm{⇒ \tau_{𝑠ℎ} = 9.55 \times\frac{𝑃_{𝑠ℎ}}{𝑁}\:Nm … (6)}$$

此外，电枢转矩和轴转矩之差称为损耗转矩，即

$$\mathrm{损耗转矩 = \tau_{a} − \tau_{𝑠ℎ} = 9.55 \times \frac{机械损耗}{𝑁}\:… (7)}$$

数值例子

一台 240 V 直流 shunt 电机吸收总电流 30 A，并以 1500 RPM 的转速运行。如果电枢和 shunt 磁场电阻分别为 0.30 Ω 和 240 Ω。求电枢产生的转矩。如果总轴输出功率为 10 马力。另外，确定电机的轴转矩和损耗转矩。

解答

这里，

$$\mathrm{分励磁场电流,\:𝐼_{sh} =\frac{240}{240}= 1 \:A}$$

$$\mathrm{电枢电流,\:𝐼_{𝑎} = 30 − 1 = 29 \:A}$$

$$\mathrm{反电动势, 𝐸_{𝑏} = 𝑉 − 𝐼_{𝑎}R_{a} = 240 − (24 \times 0.30) = 232.8 \:V}$$

因此，电枢转矩为：

$$\mathrm{\tau_{a} = 9.55 \times\frac{𝐸_𝑏𝐼_𝑎}{𝑁}= 9.55 \times (\frac{232.8 × 29}{1500 }) = 42.98\: Nm}$$

轴转矩为：

$$\mathrm{\tau_{𝑠ℎ} = 9.55 \times\frac{𝑃_{𝑠ℎ}}{𝑁}= 9.55 \times (\frac{746 \times 7}{1500} ) = 33.25 Nm}$$

损耗转矩为：

$$\mathrm{损耗转矩 = \tau_{a} − \tau_{𝑠ℎ} = 42.98 − 33.25 = 9.73 \:Nm}$$

Manish Kumar Saini

更新于：2021年8月21日

13K+ 次浏览

启动你的职业生涯

完成课程获得认证

开始学习