矢量加法的三角形法则

---

引言

矢量加法的三角形法则是一种用于加法两个矢量的概念，也称为头尾相连法。该法则还有助于计算速度、净位移和加速度。该法则有助于矢量代数，以求得两个或多个矢量之和的结果矢量R。如果将两个矢量视为P和Q，它们之间的夹角为θ，则可以使用矢量加法的三角形法则公式求出它们的和。 结果矢量R的大小|R|和方向ϕ的公式分别为：$\mathrm{|R|\: =\:\sqrt{(P^{2} + Q^{2}+ 2PQ\: cos\: θ)}}$，和 $\mathrm{ϕ \: =\: tan^{-1}[(Q\: sin \:θ)/(P \:+ \:Q \:cos \:θ)]}$。

什么是矢量加法？

矢量通常用带有箭头的线段表示，箭头指向矢量的方向，线段长度表示矢量的大小。矢量加法的三角形法则用于数学和物理学中，计算两个矢量的和，其中第一个矢量的箭头与第二个矢量的起点相连 (Zuleger, 2020)。结果矢量的大小可以表示为：R: $\mathrm{R\: =\: \sqrt{(P^{2} \:+\: 2PQ \:cos \:θ\: + \:Q^{2})}}$。结果矢量的方向可以写成：R: $\mathrm{ϕ \: =\:tan^{-1}[(Q\: sin\: θ)/(P \:+\: Q\: cos\: θ)]}$。

矢量加法的法则

由于矢量既有大小又有方向，因此不能用普通的代数方法进行加法。矢量只能用几何方法和图形方法相加。矢量加法的两个主要法则分别是三角形法则和平行四边形法则，如下所示。

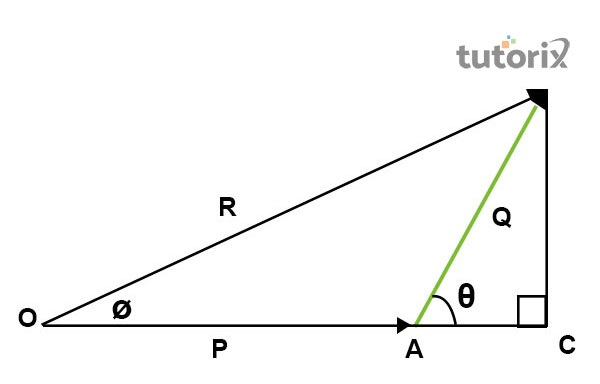
图1：矢量三角形法则

矢量三角形法则

如果两个矢量的大小和方向分别由一个三角形的两条相邻边（按顺序）表示，则称为矢量三角形法则。它们的合矢量则由该三角形的第三条边（反向）表示 (Raskin *et al.* 2021)。如上图所示，可以使用矢量三角形法则计算夹角为θ的两个矢量P和Q的合矢量。

图2：矢量平行四边形法则

矢量平行四边形法则

如果两个矢量的大小和方向分别由一个平行四边形的两条相邻边表示，则称为矢量平行四边形法则。合矢量的大小和方向由通过这两个矢量公共起点的对角线表示。如上图所示，考虑两个矢量P和Q，它们之间夹角为θ。

矢量加法三角形法则的推导

矢量加法的三角形法则有助于矢量代数，并可以推导出两个或多个矢量之和的结果矢量。例如，一辆汽车从A点行驶到B点，然后从B点行驶到C点（如下图所示）。在这种情况下，为了确定汽车的净位移，可以使用矢量加法的概念。汽车的净位移由矢量AC表示，可以使用矢量加法的三角形法则计算。

图3：矢量加法的三角形法则

在另一种情况下，有两个矢量：Q和P（如上图所示）。在这里，为了推导出矢量加法，重要的是找到这两个矢量的和。然后，移动矢量Q，使其大小和方向保持不变，并将它的起点与矢量P的终点连接起来。在这种情况下，可以使用矢量加法的三角形法则推导出矢量P和Q的和。

应用

矢量加法的三角形法则，是矢量加法的主要法则之一。矢量加法是两个不遵循普通代数法则的矢量的几何和 (De Sousa *et al.* 2017)。结果矢量可以称为矢量合成。矢量加法适用于多种情况，如下所示。

• 矢量和标量不能相加。

• 要相加的两个矢量必须具有相同的性质。例如，速度只能与速度相加，不能与力相加。

结论

如果两个矢量方向相同，则这两个矢量之间的夹角由公式计算：θ = 0°，cos 0° = 1，sin 0° = 0。这里，结果矢量的方向与每个矢量的方向相同，其大小之和等于其他矢量的大小。如果两个矢量方向相反，则这两个矢量之间的夹角由公式计算：θ = 180°，cos 180° = -1，sin 180° = 0。这里，结果矢量的大小等于两个矢量大小的差，方向与大小较大的矢量方向相同。

常见问题

Q1. 矢量求和是什么意思？

A1. 不遵循普通代数法则的多个矢量的物理求和称为矢量加法或求和。矢量加法的两个主要法则分别是矢量三角形法则和平行四边形法则。

Q2. 矢量量的例子有哪些？

A2. 既有大小又有方向的几何实体称为矢量。矢量量的例子包括位移、重量、力、速度。

Q3. 标量量是什么意思？

A3. 只有大小而没有方向的量称为标量量。这种物理量用数值表示，没有方向。

Q4. 标量量的主要例子有哪些？

A4. 标量量的主要例子包括时间、距离、质量、速度、密度、温度和体积。所有这些量都只有大小。