数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学什么是网孔电流分析法？
在这种方法中，将基尔霍夫电压定律应用于网络，根据网孔电流编写网孔方程。然后通过对该支路共有的网孔电流进行代数和来求出支路电流。
基尔霍夫电压定律
基尔霍夫电压定律（KVL）指出，在网孔中，所有电动势和电压降的代数和等于零，即：
$$\mathrm{\sum\:emfs\:+\:\sum\:Voltage\:Drops = 0}$$
网孔 - 网孔是最基本的回路形式，它不能再细分为其他回路，即网孔不包含任何内回路。
解释
每个网孔都分配一个单独的网孔电流。为方便起见，假设所有网孔电流都沿一个方向流动（顺时针或逆时针）。如果网孔电流的方向是任意的，也会得到相同的结果。
如果两个网孔电流流过一个电路元件，则该元件中的实际电流是这两个电流的代数和。
应用KVL根据网孔电流为每个网孔编写方程。在编写网孔方程时，电势升高取正号，电势降低取负号。
如果解的任何网孔电流值是负数，则意味着该网孔电流的真实方向与假设方向相反。
在下面的电路中应用KVL来编写网孔方程，如下所示：
在ABDA网孔中应用KVL，
$$\mathrm{\mathit{E}_{1}-\mathit{I}_{1}\mathit{R}_{1}-(\mathit{I}_{1}-\mathit{I}_{2})\mathit{R}_{3}=0}$$
$$\mathrm{\Rightarrow\:\mathit{E}_{1}=\mathit{I}_{1}\mathit{R}_{1}-(\mathit{I}_{1}-\mathit{I}_{2})\mathit{R}_{3}}$$
$$\mathrm{\Rightarrow\:\mathit{E}_{1}=\mathit{I}_{1}(\mathit{R}_{1}\:+\:\mathit{R}_{3})-\mathit{I}_{2}\mathit{R}_{3}}\:\:\:… (1)$$
在BCDB网孔中应用KVL，
$$\mathrm{-\mathit{I}_{2}\mathit{R}_{2}-\mathit{E}_{2}(\mathit{I}_{2}-\mathit{I}_{1})\mathit{R}_{3}=0}$$
$$\mathrm{\Rightarrow\:\mathit{E}_{2}=\mathit{I}_{1}\mathit{R}_{3}-\mathit{I}_{2}(\mathit{R}_{2}\:+\:\mathit{R}_{3})}\:\:\:… (2)$$
通过同时求解方程（1）和（2），可以得到网孔电流I1和I2。一旦得到网孔电流，就可以很容易地求出电路各支路的电流。
注意 – 网孔电流是虚构的量，无法测量。而支路电流是实际电流，因为它们实际上流过支路，可以测量。
数值例子
计算下面电路中每个支路的电流。
解答
分别为ABDA和BCDB网孔分配网孔电流I1和I2，如下图所示。
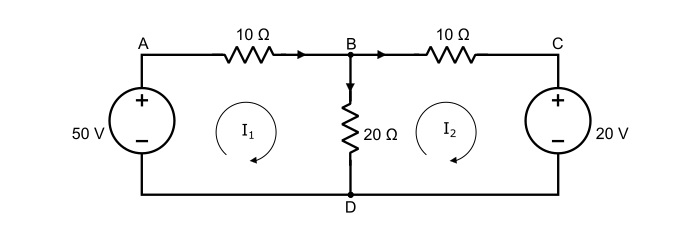
将KVL应用于ABDA网孔，
$$\mathrm{50-10\mathit{I}_{1}-20(\mathit{I}_{1}-\mathit{I}_{2})=0}$$
$$\mathrm{\Rightarrow\:50=30\mathit{I}_{1}-20\mathit{I}_{2}}$$
$$\mathrm{3\mathit{I}_{1}-2\mathit{I}_{2}=5\:\:\:… (3)}$$
将KVL应用于BCDB网孔，
$$\mathrm{-10\mathit{I}_{2}-20-20(\mathit{I}_{2}-\mathit{I}_{1})=0}$$
$$\mathrm{\Rightarrow\:-30\mathit{I}_{2}+20\mathit{I}_{1}=20}$$
$$\mathrm{2\mathit{I}_{1}-3\mathit{I}_{2}=2\:\:\:… (4)}$$
同时求解方程（3）和（4），网孔电流I1和I2为：
$$\mathrm{\mathit{I}_{1}=2.2\:A\:and\:\mathit{I}_{2}=0.8\:A}$$
因此，支路电流将为：
$$\mathrm{DAB支路的电流=\mathit{I}_{1}=2.2\:A\:\:\:(从A流向B)}$$
$$\mathrm{BCD支路的电流=\mathit{I}_{2}=0.8\:A\:\:\:(从B流向C)}$$
$$\mathrm{BD支路的电流=(\mathit{I}_{1}-I_{2})=2.2 − 0.8 = 1.4\:A\:\:\:(从B流向D)}$$
浏览量：531
