数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究什么是节点分析？
节点分析是一种确定电路中支路电流的方法。在这种方法中，一个节点被选为参考节点。电路中所有节点的电位都相对于此参考节点测量。
节点分析基于基尔霍夫电流定律，该定律指出“节点处所有进入电流和离开电流的代数和等于零”。
$$\mathrm{\sum\:\mathit{I}_{incoming}\:+\:\sum\:\mathit{I}_{outgoing}=0}$$
节点 – 节点是网络中两个或多个电路元件连接的点。
结点 – 结点是三个或多个电路元件连接的点。
在节点分析中，我们必须找到结点处的电位而不是节点处的电位。所需的独立节点对方程数比网络中结点数少一个。也就是说，如果“n”是独立节点方程数，“j”是结点数，则：
$$\mathrm{n\:=\:\mathit{j}\:-\:1}$$
解释
考虑以下所示的电路。在电路中，A、B、C 和 D 是四个节点，节点 B 和 D 是结点，其中节点 D 被选为参考节点。因此，
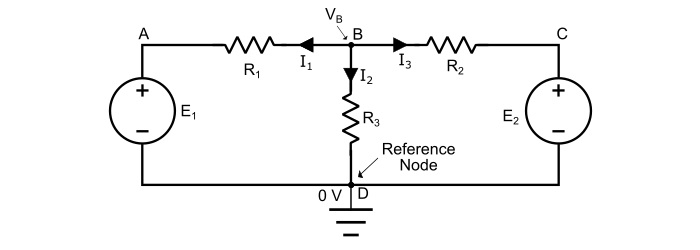
假设节点 B 处的电压 VB 高于电路中所有其他节点。
在节点 B 处应用 KCL，我们得到：
$$\mathrm{\mathit{I}_{1}\:+\:\mathit{I}_{2}\:+\:\mathit{I}_{3}=0}\:\:\:…(1)$$
现在，根据欧姆定律，支路电流为：
$$\mathrm{\mathit{I}_{1}=\frac{\mathit{V}_{B}\:-\mathit{E}_{1}\:-0}{\mathit{R}_{1}}=\frac{\mathit{V}_{B}\:-\:E_{1}}{\mathit{R}_{1}}}$$
$$\mathrm{\mathit{I}_{2}=\frac{\mathit{V}_{B}\:-\mathit{E}_{2}\:-0}{\mathit{R}_{2}}=\frac{\mathit{V}_{B}\:-\:E_{2}}{\mathit{R}_{2}}}$$
并且，
$$\mathrm{\mathit{I}_{3}=\frac{\mathit{V}_{B}\:-0}{\mathit{R}_{3}}=\frac{\mathit{V}_{B}}{\mathit{R}_{3}}}$$
将 I1、I2 和 I3 的值代入方程 (1)，我们得到：
$$\mathrm{\frac{\mathit{V}_{B}\:-\mathit{E}_{1}}{\mathit{R}_{1}}+\frac{\mathit{V}_{B}\:-E_{2}}{\mathit{R}_{2}}+\frac{\mathit{V}_{B}}{\mathit{R}_{3}}=0}\:\:\:…(2)$$
可以通过求解方程 (2) 获得节点 B 处的电压 VB。由于电动势 E1、E2 和电阻值是已知的。因此，我们可以确定支路电流的值。
数值示例
使用节点分析法求解下图所示电路中各支路的电流。
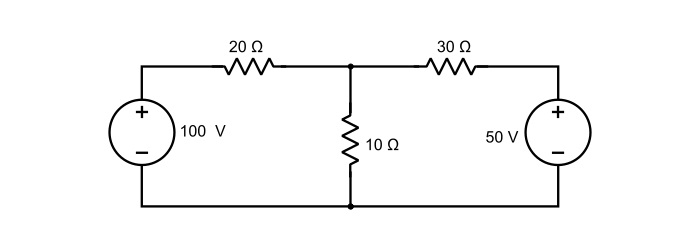
解答
在电路图中标记各支路的电流。如果解出的任何电流值为负数，则表示电流的实际方向与假设方向相反。取点 B 作为参考节点。因此，
在节点 A 处应用 KCL，
$$\mathrm{\mathit{I}_{1}\:+\:\mathit{I}_{2}\:+\:\mathit{I}_{3}=0}\:\:\:…(3)$$
根据欧姆定律，
$$\mathrm{\mathit{I}_{1}=\frac{\mathit{V}_{A}-100}{20}}$$
$$\mathrm{\mathit{I}_{2}=\frac{\mathit{V}_{A}}{10}}$$
并且
$$\mathrm{\mathit{I}_{3}=\frac{\mathit{V}_{A}-50}{30}}$$
将 I1、I2 和 I3 的值代入方程 (3)，我们得到：
$$\mathrm{\frac{\mathit{V}_{A}-100}{20}+\frac{\mathit{V}_{A}}{10}+\frac{\mathit{V}_{A}-50}{30}=0}$$
$$\mathrm{\Rightarrow\frac{3(\mathit{V}_{A}-100)+6\mathit{V}_{A}+2(\mathit{V}_{A}-50)}{60}=0}$$
$$\mathrm{\Rightarrow\:3\mathit{V}_{A}-300+6\mathit{V}_{A}+2\mathit{V}_{A}-100=0}$$
$$\mathrm{\Rightarrow\:11\mathit{V}_{A}=400}$$
$$\mathrm{\mathit{V}_{A}=\frac{400}{11}=36.36\mathit{V}}$$
因此，节点 A 处的电压等于 36.36 V，因此支路电流为：
$$\mathrm{电流\:\mathit{I}_{1}=\frac{\mathit{V}_{A}-100}{20}=\frac{36.36-100}{20}=-3.182\:A}$$
$$\mathrm{电流\:\mathit{I}_{2}=\frac{\mathit{V}_{A}}{20}=\frac{36.36}{20}=3.636\:A}$$
$$\mathrm{电流\:\mathit{I}_{3}=\frac{\mathit{V}_{A}-50}{30}=\frac{36.36-50}{30}=0.455\:A}$$
电流 I1 和 I3 的负号表示电流的实际方向与假设方向相反。
1K+ 浏览量
