无线信道噪声：噪声功率的解题

在本节中，我们将根据白噪声模型解决一些关于无线信道噪声的问题。

例题 1

一个白噪声的双边功率谱密度为 6 kW/MHz。它通过一个带宽为 1 kHz 的低通滤波器。计算输出噪声功率。

解答 -

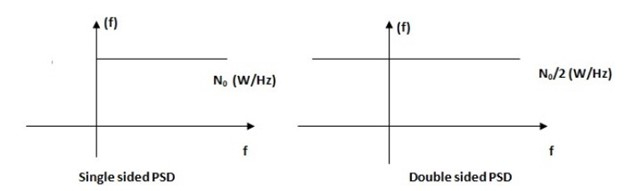
双边功率谱密度为 6 kW/MHz。功率谱密度通常以 W/Hz 表示。

$$\frac{6kW}{MHz}=\frac{6000W}{1000000Hz}=\frac{0.006W}{Hz}=\frac{N_{0}}{2}$$

双边功率谱密度 N0/2 为 0.006W/Hz。因此，N0 = 0.012W/Hz。

噪声功率表示为噪声功率谱密度和噪声带宽的乘积。

$$N_{p}=N_{0}.BW$$

$$N_{p}=\frac{0.012W}{Hz}.1kHz=12W$$

该系统的噪声功率为 12W

例题 2

一个复合电视信号的带宽为 40 MHz，并以 0.1 W 的功率通过卫星信道传输。白噪声的双边功率谱密度为 10^-15 W/Hz。该链路的噪声功率是多少？

解答 - 噪声功率表示为系统带宽和噪声功率谱密度的乘积。噪声将存在于信号传输的频率范围内。因此，信号带宽等于噪声带宽。

可以使用给定数据找到噪声的单边功率谱密度。

$$\frac{N_{0}}{2}=10^{-15}\frac{W}{Hz}\Rightarrow\:N_{0}=2\times\:10^{-15}W/Hz$$

使用给定的值，我们发现噪声功率为

$$(40\times\:10^{6}).(2\times\:10^{-15})W=80nW$$

例题 3

通信接收机输出端可用的噪声电平为 -10 dBm。绝对尺度上的噪声电平是多少？

解答 - 绝对尺度上的噪声功率计算如下：

$$10log_{10}(\frac{N_{p}}{1mW})=-10dBm$$

$$log_{10}(\frac{N_{p}}{1mW})=-1\Rightarrow\:\frac{N_{p}}{1mW}=10^{-1}$$

$$N_{p}=10^{-1}mW=100\mu\:W$$

因此，噪声功率为 100 微瓦

Venkataraman S

更新于： 2021年6月23日

949 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习