数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究二维矩阵中的最大和矩形
给定一个矩阵。我们需要找出矩形（有时为正方形）矩阵，其和最大。
此算法的思想是固定左右列，然后为每一行尝试找出从左列到右列元素的和，并临时存储它。我们将尝试找出顶部和底部行号。获得临时数组后，我们可以应用 Kadane 算法来查找最大和子数组。这样，整个矩形就形成了。
输入和输出
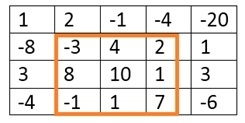
Input: The matrix of integers. 1 2 -1 -4 -20 -8 -3 4 2 1 3 8 10 1 3 -4 -1 1 7 -6 Output: The top left point and bottom right point of the submatrix, and the total sum of the submatrix. (Top, Left) (1, 1) (Bottom, Right) (3, 3) The max sum is: 29
算法
kadaneAlgorithm(array, start, end, n)
输入：数组将保存和、开始和结束点、元素数量。
输出 − 找出起点和终点。
Begin sum := 0 and maxSum := - ∞ end := -1 tempStart := 0 for each element i in the array, do sum := sum + array[i] if sum < 0, then sum := 0 tempStart := i + 1 else if sum > maxSum, then maxSum := sum start := tempStart end := i done if end ≠ -1, then return maxSum maxSum := array[0], start := 0 and end := 0 for each element i from 1 to n of array, do if array[i] > maxSum, then maxSum := array[i] start := i and end := i done return maxSum End
maxSumRect(Matrix)
输入：给定的矩阵。
输出：矩形的最大和。
Begin maxSum := - ∞ define temp array, whose size is same as row of matrix for left := 0 to number of columns in the Matrix, do till temp array with 0s for right := left to column of matrix -1, do for each row i, do temp[i] := matrix[i, right] done sum := kadaneAlgorithm(temp, start, end, number of rows) if sum > maxSum, then maxSum := sum endLeft := left endRight := right endTop := start endBottom := end done done display top left and bottom right corner and the maxSum End
示例
#include<iostream>
#define ROW 4
#define COL 5
using namespace std;
int M[ROW][COL] = {
{1, 2, -1, -4, -20},
{-8, -3, 4, 2, 1},
{3, 8, 10, 1, 3},
{-4, -1, 1, 7, -6}
};
int kadaneAlgo(int arr[], int &start, int &end, int n) { //find max sum and starting and ending location
int sum = 0, maxSum = INT_MIN;
end = -1; //at first no place is selected
int tempStart = 0; //starting from 0
for (int i = 0; i < n; i++) {
sum += arr[i];
if (sum < 0) {
sum = 0;
tempStart = i+1;
}else if (sum > maxSum) { //get maximum sum, and update start and end index
maxSum = sum;
start = tempStart;
end = i;
}
}
if (end != -1)
return maxSum;
//when all elements are negative in the array
maxSum = arr[0];
start = end = 0;
// Find the maximum element in array
for (int i = 1; i < n; i++) {
if (arr[i] > maxSum) {
maxSum = arr[i];
start = end = i;
}
}
return maxSum;
}
void maxSumRect() {
int maxSum = INT_MIN, endLeft, endRight, endTop, endBottom;
int left, right;
int temp[ROW], sum, start, end;
for (left = 0; left < COL; left++) {
for(int i = 0; i<ROW; i++)//temp initially holds all 0
temp[i] = 0;
for (right = left; right < COL; ++right) {
for (int i = 0; i < ROW; ++i) //for each row, find the sum
temp[i] += M[i][right];
sum = kadaneAlgo(temp, start, end, ROW); //find sum of rectangle (top, left) and (bottom right)
if (sum > maxSum) { //find maximum value of sum, then update corner points
maxSum = sum;
endLeft = left;
endRight = right;
endTop = start;
endBottom = end;
}
}
}
cout << "(Top, Left) ("<<endTop<<", "<<endLeft<<")"<<endl;
cout << "(Bottom, Right) ("<<endBottom<<", "<<endRight<<")"<<endl;
cout << "The max sum is: "<< maxSum;
}
int main() {
maxSumRect();
}输出
(Top, Left) (1, 1) (Bottom, Right) (3, 3) The max sum is: 29
更新日期： 2020 年 6 月 17 日
1 千次以上浏览
广告