数据结构
网络
关系型数据库管理系统(RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学(a) 什么是远视？说明远视（或远视眼）的两个原因。借助光线图，展示：(i) 远视眼的缺陷。(ii) 使用透镜矫正远视。(b) 一只眼睛的近点距离为 0.75 米。需要什么样的眼镜镜片才能将近点距离减小到 0.25 米？还需要计算所需的镜片度数。这只眼睛是远视还是近视？(c) 一只眼睛的远点为 2 米。需要什么样的眼镜镜片才能将远点增加到无限远？还需要计算所需的镜片度数。这只眼睛是远视还是近视？
(a) 远视，或远视眼，是一种视觉缺陷，由于这种缺陷，一个人无法看清近处的物体，但远处的视力正常。
远视（或远视眼）的两个原因如下：
1. 眼球晶状体的会聚能力低（由于其焦距较长），导致物体成像在视网膜后方；或
2. 眼球太短，导致光线聚焦在视网膜后方，而不是直接在视网膜上。
(i) 显示远视眼缺陷的光线图。
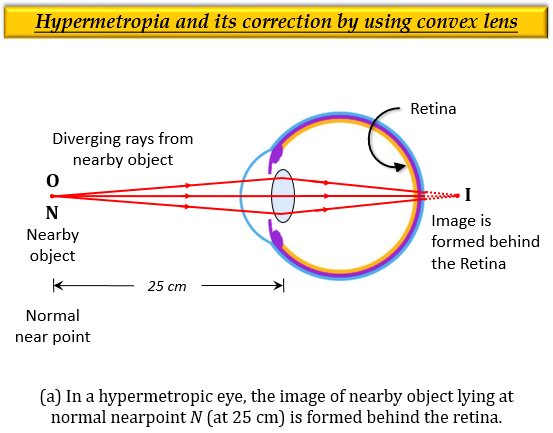
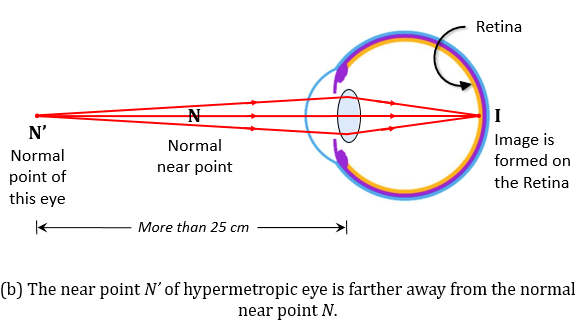
(ii) 显示使用透镜矫正远视的光线图。
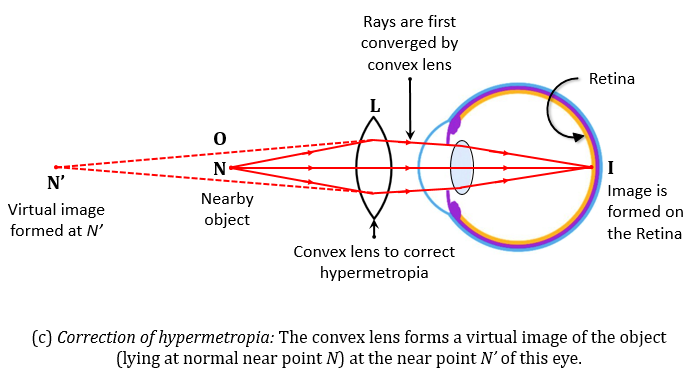
(b) 一只眼睛的近点距离为 0.75 米（或 75 厘米），这意味着它是一只远视眼，因为远视眼的近点大于 0.25 米（或 25 厘米）。
为了矫正远视缺陷，应使用带有凸透镜的眼镜。
为了找到所需的凸透镜的度数，首先，我们必须计算其焦距。
已知
远视者的近点为 0.75 米（如果物体的像在离眼睛 0.75 米的远视者自己的近点处形成，则该人可以看到放置在眼睛前方 0.25 米的正常近点处的物体）。
物体距离，$u$ = $−$0.25 米（物体在正常近点处的距离）
像距，$v$ = $−$0.75 米（缺陷眼在透镜前方的近点）
求：焦距，$f$，和透镜度数，$P$。
解答
从透镜公式我们知道：
$\frac {1}{v}-\frac {1}{u}=\frac {1}{f}$
代入给定值，我们得到：
$\frac {1}{(-0.75)}-\frac {1}{(-0.25)}=\frac {1}{f}$
$-\frac {100}{75}+\frac {100}{25}=\frac {1}{f}$
$-\frac {4}{3}+\frac {4}{1}=\frac {1}{f}$
$\frac {-4+12}{3}=\frac {1}{f}$
$\frac {8}{3}=\frac {1}{f}$
$f=\frac {3}{8}$
$f=+0.375m=+37.5cm$
因此，焦距 $f$ 为 37.5 厘米。
现在，
我们知道透镜的度数表示为：
$P=\frac {1}{f}$
代入 $f$ 的值，我们得到：
$P=\frac {1}{0.375}$
$P=\frac {1000}{375}$
$P=+2.67D$
因此，矫正该缺陷所需的凸透镜的度数为 +2.67 二极管。
这只眼睛是远视的，因为透镜的度数为正号 $(+)$，这意味着它是凸透镜，我们知道凸透镜用于矫正远视或远视眼。
(c) 一只眼睛的远点距离为 2 米（或 200 厘米），这意味着它是一只近视眼，因为近视眼的远点小于无限远。
为了矫正近视缺陷，应使用带有凹透镜的眼镜。
为了找到所需的凹透镜的度数，首先，我们必须计算其焦距。
已知
近视者的远点为 2 米（如果物体的像在离眼睛 2 米的近视者自己的远点处形成，则该人可以看到放置在正常近点 0.25 米处的物体）。
物体距离，$u$ = $\infty$
像距，$v$ = $−$2 米（缺陷眼在透镜前方的远点）
求：焦距，$f$，和透镜度数，$P$。
解答
从透镜公式我们知道：
$\frac {1}{v}-\frac {1}{u}=\frac {1}{f}$
代入给定值，我们得到：
$\frac {1}{(-2)}-\frac {1}{\infty}=\frac {1}{f}$
$-\frac {1}{2}-0=\frac {1}{f}$ $(\because 任何数除以无穷大都等于 0)$
$-\frac {1}{2}=\frac {1}{f}$
$f=-2m$
因此，焦距 $f$ 为 -2 米。
现在，
我们知道透镜的度数表示为：
$P=\frac {1}{f}$
代入 $f$ 的值，我们得到：
$P=\frac {1}{-2}$
$P=-0.5D$
因此，矫正该缺陷所需的凹透镜的度数为 -0.5 二极管。
这只眼睛是近视的，因为透镜的度数为负号 $(-)$，这意味着它是凹透镜，我们知道凹透镜用于矫正近视或近视眼。
540 次浏览
