数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
Microsoft Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学基于鸢尾花数据集的决策树和K均值聚类分析
决策树和K均值聚类算法是数据科学和机器学习中常用的技术，用于从大型数据集（如鸢尾花数据集）中发现模式和洞察力。众所周知，人工智能广泛应用于我们的日常生活中，从在移动设备上阅读新闻到分析工作中的复杂数据。人工智能提高了人类工作的速度、准确性和效率。人工智能的发展使我们能够完成以前被认为不可能的事情。
在这篇文章中，我们将学习决策树算法和K均值聚类算法，以及如何在鸢尾花数据集上应用它们。
鸢尾花数据集
费雪的鸢尾花数据集是一个多元数据集，由英国统计学家和生物学家罗纳德·费雪在他1936年的著作《在分类问题中使用多种测量》中作为线性判别分析的例子而闻名。费雪的工作发表在该期刊上。埃德加·安德森收集了这些数据，以研究三种密切相关的鸢尾花物种的花朵之间存在的形态差异。在加斯佩半岛，这三个物种中的两个物种是“在同一天，同一个人使用相同的测量设备，从同一个牧场收集的”。
该数据集包含从三个鸢尾花物种（山鸢尾、维吉尼亚鸢尾和变色鸢尾）中收集的50个样本。对每个样本都测量了萼片和花瓣的长度和宽度（以厘米为单位）。这是测量的四个特征中的两个。
决策树
决策树是一种非参数的监督学习方法，常用于分类和回归应用。它具有类似树的分层结构，由根节点、分支、内部节点和叶节点组成。
K均值聚类
K均值聚类是一种向量量化技术，起源于信号处理领域。其目标是将n个观测值分成k个聚类，使得每个观测值都属于具有最近均值（聚类中心或聚类质心）的聚类，该均值充当聚类的原型。这导致数据空间被划分为Voronoi单元。虽然几何中位数是唯一可以最小化欧几里得距离的，但均值是针对平方误差优化的。例如，可以使用k-medians和k-medoids找到改进的欧几里得解。
在鸢尾花数据集上应用决策树和K均值聚类算法
示例
import pandas as pdd from sklearn import datasets import numpy as npp import sklearn.metrics as smm import matplotlib.patches as mpatchess from sklearn.cluster import KMeans import matplotlib.pyplot as pltt from sklearn.metrics import accuracy_score %matplotlib inline iris = datasets.load_iris() print(iris.target_names) print(iris.target) x1 = pdd.DataFrame(iris.data, columns=['Sepal Length', 'Sepal Width', 'Petal Length', 'Petal Width']) y1 = pdd.DataFrame(iris.target, columns=['Target']) x1.head()
输出
['setosa' 'versicolor' 'virginica']
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
Sepal Length Sepal Width Petal Length Petal Width
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2
3 4.6 3.1 1.5 0.2
4 5.0 3.6 1.4 0.2
打印目标变量y的前5行：
y1.head()
输出
Target 0 0 1 0 2 0 3 0 4 0
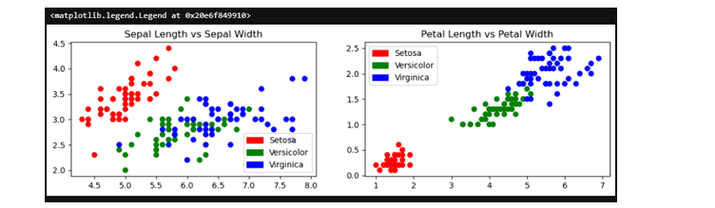
下一步，绘制数据集图，显示数据集变量之间的差异：
pltt.figure(figsize=(12,3))
colors = npp.array(['red', 'green', 'blue'])
iris_targets_legend = npp.array(iris.target_names)
red_patch = mpatchess.Patch(color='red', label='Setosa')
green_patch = mpatchess.Patch(color='green', label='Versicolor')
blue_patch = mpatchess.Patch(color='blue', label='Virginica')
pltt.subplot(1, 2, 1)
pltt.scatter(x1['Sepal Length'], x1['Sepal Width'], c=colors[y1['Target']])
pltt.title('Sepal Length vs Sepal Width')
pltt.legend(handles=[red_patch, green_patch, blue_patch])
pltt.subplot(1,2,2)
pltt.scatter(x1['Petal Length'], x1['Petal Width'], c= colors[y1['Target']])
pltt.title('Petal Length vs Petal Width')
pltt.legend(handles=[red_patch, green_patch, blue_patch])
输出
下一步我们将定义聚类。
iris_k_mean_model = KMeans(n_clusters=3) iris_k_mean_model.fit(x1) print(iris_k_mean_model.labels_)
输出
KMeans(n_clusters=3) [[5.9016129 2.7483871 4.39354839 1.43387097] [5.006 3.428 1.462 0.246 ] [6.85 3.07368421 5.74210526 2.07105263]]
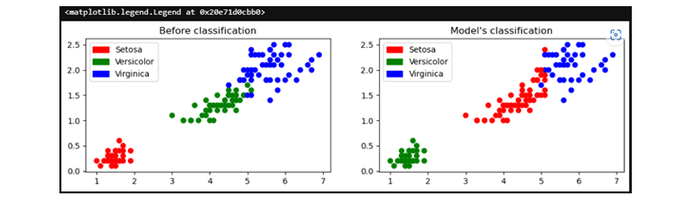
现在，我们将绘制分类前后的图形：
pltt.figure(figsize=(12,3))
colors = npp.array(['red', 'green', 'blue'])
predictedY = npp.choose(iris_k_mean_model.labels_, [1, 0, 2]).astype(npp.int64)
pltt.subplot(1, 2, 1)
pltt.scatter(x1['Petal Length'], x1['Petal Width'], c=colors[y1['Target']])
pltt.title('Before classification')
pltt.legend(handles=[red_patch, green_patch, blue_patch])
pltt.subplot(1, 2, 2)
pltt.scatter(x1['Petal Length'], x1['Petal Width'], c=colors[predictedY])
pltt.title("Model's classification")
pltt.legend(handles=[red_patch, green_patch, blue_patch])
输出
下一步，我们将打印模型的准确性：
smm.accuracy_score(predictedY, y1['Target'])
输出
0.24
下一步，我们将测试模型并打印测试数据集和训练数据集的准确性：
from sklearn.metrics import accuracy_score
X = iris.data
# Extracting Target / Class Labels
y = iris.target
# Import Library for splitting data
from sklearn.model_selection import train_test_split
# Creating Train and Test datasets
X_train, X_test, y_train, y_test = train_test_split(X,y, random_state = 50, test_size = 0.25)
# Creating Decision Tree Classifier
from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier()
clf.fit(X_train,y_train)
# Predict Accuracy Score
y_pred = clf.predict(X_test)
print("Train data accuracy:",accuracy_score(y_true = y_train, y_pred=clf.predict(X_train)))
print("Test data accuracy:",accuracy_score(y_true = y_test, y_pred=y_pred))
输出
Train data accuracy: 1.0 Test data accuracy: 0.9473684210526315
结论
总之，鸢尾花数据集是一个常用的机器学习数据集，常用于测试不同的算法。在这里，我们使用了流行的决策树算法和K均值聚类算法来分析数据。
通过使用这些方法，我们可以更好地了解数据的结构，并利用该结构进行预测和对数据进行分组。
浏览量：572
