使用 SciPy 通过将随机数据分成 2 个簇来实现 K 均值聚类？

K 均值聚类算法，也称为扁平聚类，是一种计算一组未标记数据中的簇和簇中心（质心）的方法。它会不断迭代，直到找到最佳质心。对于一个簇，我们可以认为它是一组数据点，其点间距离与簇外点到该簇的距离相比很小。在 K 均值算法中，“K”表示从未标记数据中标识出的簇数。

给定一组最初的 K 个中心后，可以通过执行以下步骤使用 SciPy 库完成 K 均值聚类算法 −

步骤 1− 数据点规范化

步骤 2− 计算称为代码的质心。在此处，二位质心数组称为码本。

步骤 3− 形成簇和分配数据点。这意味着从码本进行映射。

示例

#importing the required Python libraries :
import numpy as np
from numpy import vstack,array
from numpy.random import rand
from scipy.cluster.vq import whiten, kmeans, vq
from pylab import plot,show

#Random data generation :
data = vstack((rand(200,2) + array([.5,.5]),rand(150,2)))

#Normalizing the data :
data = whiten(data)

# computing K-Means with K = 2 (2 clusters)
centroids, mean_value = kmeans(data, 2)
print("Code book :", centroids, "")
print("Mean of Euclidean distances :", mean_value.round(4))

# mapping the centroids
clusters, _ = vq(data, centroids)
print("Cluster index :", clusters, "")
#Plotting using numpy's logical indexing
plot(data[clusters==0,0],data[clusters==0,1],'ob',data[clusters==1,0],data[clusters==1,1],'or')
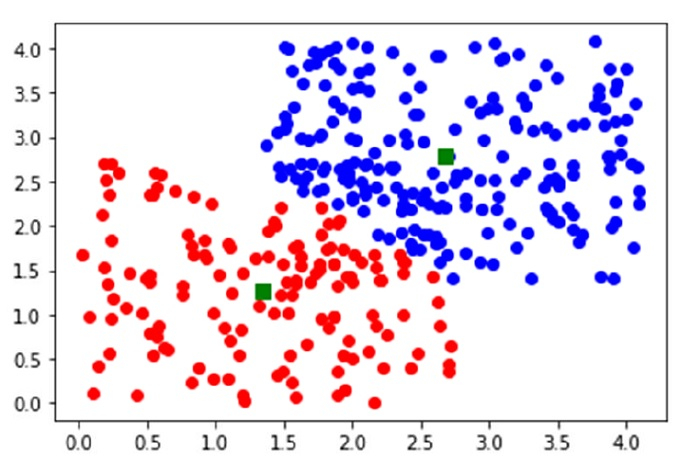
plot(centroids[:,0],centroids[:,1],'sg',markersize=8)
show()

输出

Code book :
[[2.68379425 2.77892846]
[1.34079677 1.27029728]]


Mean of Euclidean distances : 0.9384

Cluster index : [0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 1 0 0 1 1 0
0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1
0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 1 0 1 0 1 1 1 1 0 1 1 1 1 0 1 1 1 1 1
1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 0 1 1
1 1 1 1 1 1 1 0 1 1 1 0 1 0 1 1 1 1 1 0 1 0 1 1 1 0 1 0 1 1 1 1 1 1 1 1 0
1 1 1 1 1 0 1 1 0 0 0 1 1 1 1 1 1 1 1 1 1 1 0 1 1 0 0 1 1 0 0 1 0 1 1 1 1
1 1 0 1 1 1 1 1 1 0 1 1 0 1 1 1 0]

Gaurav Kumar

更新于:14-Dec-2021

1360 次查看

开启您的 职业生涯

完成课程以获得认证

开始