如果一个物体的形状可以分成两个完全相同的碎片,则该物体具有对称性。在对称形状中,一半是另一半的镜像。当我们画一条线穿过图中给出的每个形状的中心点以检查其对称性时,我们发现:$(a)$。它有一条对称线。$(b)$。它有一条对称线。$(c)$。它有一条对称线。$(d)$。它有一条对称线。$(e)$。它有四条对称线。$(f)$。它有一条对称线。$(g)$。它有一条对称线。$(h)$。它有一条对称线。$(i)$。它有一条对称线。$(j)$。它 ... 阅读更多
反射对称性是一种对称性,其中物体的一半反映了物体的另一半。它也被称为镜像对称性。对称线可以是任何方向,水平、垂直、倾斜等。$(a)$。垂直对称性 - A、H、I、M、O、T、U、V、W、X、Y$(b)$。水平对称性 - B、C、D、E、H、I、K、O、X$(c)$。水平和垂直对称性 - O、X、I、H
已知:$(a)$。等腰三角形?$(b)$。圆形?任务:写出可以赋予给定形状的对称线的另一个名称。解决方案:众所周知,等腰三角形只有一条对称线,这条线是连接顶点与其对面边中点的线段,并且平分它。因此,我们可以称之为中线。圆形有无数条穿过圆心的对称线,因此我们当然可以称之为直径。因此,可以赋予以下对称线的另一个名称$(a)$。等腰三角形的中线是 ... 阅读更多
任务:给出三个没有对称线的形状的例子。解决方案:对称线是一条将物体分成两半的线。当一个图形对折时,两个半部分在其对称线上完全重合。这条对称线称为对称轴。如下所示,斜三角形、平行四边形和梯形没有对称线,因为没有一条线可以将这些图形分成两个相等的图形。
已知:$(i)$. $2^6$$(ii)$. $9^3$$(iii)$. $11^2$$(iv)$. $5^4$任务:求出给定项的值。解决方案:$(i)$. $2^6$$=2\times2\times2\times2\times2\times2$$=64$$(ii)$. $9^3$$=9\times9\times9$$=729$$(iii)$. $11^2$$=11\times11$$=121$$(iv)$. $5^4$$=5\times5\times5\times5$$=625$
已知:$(i)$. $6\times6\times6\times6$$(ii)$. $t\times t$$(iii)$. $b\times b\times b\times b$$(iv)$. $5\times5\times7\times7\times7$$(v)$. $2\times2\times a\times a$$(vi)$. $a\times a\times a\times c\times c\times c\times c\times d$任务:将给定项写成指数形式。解决方案:$(i)$. $6\times6\times6\times6$$=6^4$$(ii)$. $t\times t$$=t^2$$(iii)$. $b\times b\times b\times b$$=b^4$$(iv)$. $5\times5\times7\times7\times7$$=5^{2\ }\times7^3$$(v)$. $2\times2\times a\times a$$=2^2\times a^2$$(vi)$. $a\times a\times a\times c\times c\times c\times c\times d$$=a^3\times c^4\times d$阅读更多
已知:给定的数字是 $(i).\ 3125$ $(ii).\ 729$ $(iii).\ 343$ $(iv).\ 512$。任务:我们将给定的数字表示成指数形式。解决方案:$(i).\ 512$$512 = 8 \times 8\times 8 = 8^3$因此,512 的指数形式是 $8^3$。 $(ii).\ 343$$343 = 7 \times 7\times 7 = 7^3$因此,343 的指数形式是 $7^3$。$(iii).\ 729$$729 = 3 \times 3\times 3\times 3 \times 3 \times 3 = 3^6$因此,729 的指数形式是 $3^6$。$(iv).\ 3125$$3125 = 5 \times 5\times 5\times 5 \times 5 = 5^5$因此,3125 的指数形式是 $5^5$。
已知:$(i)$. $4^{3}$ 或 $3^4$$(ii)$. $5^3$ 或 $3^5$$(iii)$. $2^8$ 或 $8^2$$(iv)$. $100^2$ 或 $2^{100}$$(v)$. $2^{10}$ 或 $10^2$任务:在每种情况下尽可能地找出较大的数字。解决方案: $(i)$. $4^3$ 或 $3^4$$4^3=4\times4\times4$$=64$现在,$3^4=3\times3\times3\times3$$=81$由于,$64$$100$因此,$2^{10}$>$10^2$
已知:$(i)$. $2\times10^3$$(ii)$. $7^2\times2^2$$(iii)$. $2^3\times5$$(iv)$. $3\times4^4$$(v)$. $0\times10^2$$(vi)$. $5^2\times3^3$$(viii)$. $2^4\times3^2$$(viii)$. $3^2\times10^4$任务:化简给定的数字。解决方案:$(i)$. $2\times10\times10\times10=2000$$(ii)$. $7\times7\times2\times2=196$$(iii)$. $2\times2\times2\times5=40$$(iv)$. $3\times4\times4\times4\times4=768$$(v)$. $0\times10\times10=0$$(vi)$. $5\times5\times3\times3\times3=675$$(viii)$. $2\times2\times2\times2\times3\times3=144$$(viii)$. $3\times3\times10\times10\times10\times10=90000$
已知:$(i)$. $(-4)^3$$(ii)$. $(-3)\times(-2)^3$$(iii)$. $(-3)^2\times(-5)^2$$(iv)$. $(-2)^3\times(-10)^3$任务:化简给定项。解决方案:$(i)$. $(-4)^3$$=-4\times-4\times-4$$=-64$$(ii)$. $(-3)\times(-2)^3$$=(-3)\times(-2)\times(-2)\times(-2)$$=24$$(iii)$. $(-3)^2\times(-5)^2$$=(-3)\times(-3)\times(-5)\times(-5)$$=225$$(iv)$. $(-2)^3\times(-10)^3$$=(-2)\times(-2)\times(-2)\times(-10)\times(-10)\times(-10)$$=8000$

 数据结构
数据结构 网络
网络 关系数据库管理系统
关系数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 编程
C 编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP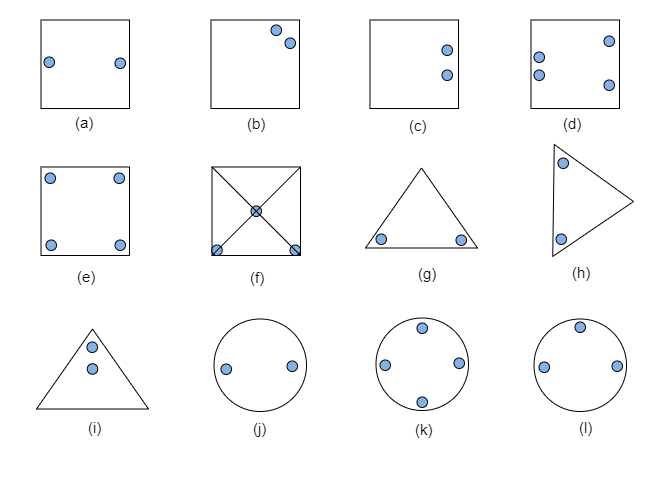 "\
"\