数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学
你需要证明 $∆AMP ≅ ∆AMQ$。在下述证明中，补充缺失的理由。步骤 理由
| 步骤 | 理由 |
| $(i).\ PM = QM$ | $(i)$ …… |
| $(ii).\ \angle PMA = \angle QMA$ | $(ii)$ …… |
| $(iii).\ AM = AM$ | $(iii)$ …… |
| $(iv).\ ∆AMP ≅ ∆AMQ$ | $(iv)$ …… |
步骤 理由 $(i).\ PM = QM$ $(i)$ 题目已知 $(ii).\ \angle PMA = \angle QMA$ $(ii)$ 题目已知 $(iii).\ AM = AM$ $(iii)$ 公共边 $(iv).\ ∆AMP ≅ ∆AMQ$ $(iv)$ SAS全等定理
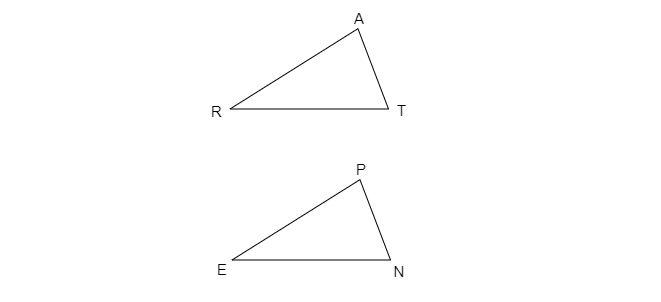
$(a)$ 当且仅当一个三角形的所有三条边都等于另一个三角形的所有三条边时，这两个三角形根据SSS定理全等。因此，如果根据SSS定理 $∆ ART ≅ ∆ PEN$，则 $(i).\ AR=PE$ $(ii).\ RT=EN$ 和 $(iii).\ AT=PN$ $(b)$ 当且仅当一个三角形的两条边及其夹角等于另一个三角形的两条边及其夹角时，这两个三角形根据SAS定理全等。因此，如果根据SAS定理 $∆ ART ≅ ∆ PEN$，并且给出…… 阅读更多
已知：$∆DEF ≅ ∆BCA$。需要：写出与 $(i).\ \angle E$ $(ii).\ \overline{EF}$ $(iii).\ \angle F$ $(iv).\ \overline{DF}$ 对应的 $∆BCA$ 部分。解答：已知 $∆ DEF ≅ ∆ BCA$。由于我们知道全等三角形的对应部分相等，因此我们可以说两个全等三角形的对应边和角相等。(i). $∠E=∠C$ (ii). 边 $EF=$边 $CA$ (iii). $∠F=∠A$ (iv). 边 $DF=$边 $BA$
当一个形状放置在另一个形状上，如果它们互相重叠，则称它们全等。如果两个图形具有相同的形状和大小，则它们是全等的。两个全等形状的现实生活例子是：(1) 同一品牌同一型号的两部手机是全等形状的例子。(2) 两本七年级的 NCERT 科学教科书。
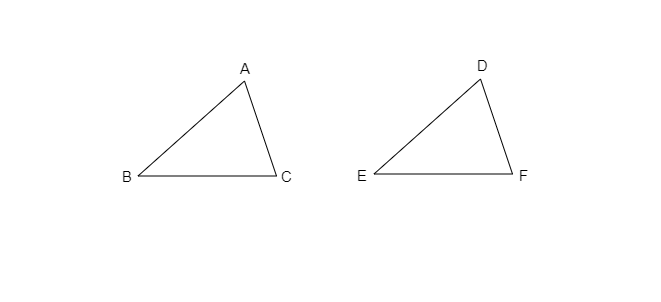
$(a)$. 已知：$AC = DF$ $AB = DE$ $BC = EF$ 所以，证明 $∆ABC ≅ ∆DEF$ 的全等准则为 SSS（边边边）全等。 $(b)$ 已知：$ZX = RP$ $RQ = ZY$ $\angle PRQ = \angle XZY$ 所以，证明 $∆PQR ≅ ∆XYZ$ 的全等准则为 SAS（边角边）全等。 $(c)$. 已知：$\angle MLN = \angle FGH$ $\angle NML = \angle GFH$ $ML = FG$ 所以，证明 $∆LMN ≅ ∆GFH$ 的全等准则为 AAS（角角边）全等。 $(d)$ 已知：$EB = DB$ $AE = BC$ $\angle A = \angle C = 90^{\circ}$ 所以，证明 $∆ABE ≅ ∆CDB$ 的全等准则为 SAS（边角边）全等。
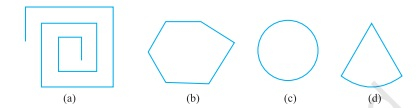
需要：我们需要找到所给物体的形状。解答：(a) 文具盒的形状是长方体。(b) 砖块的形状是长方体。(c) 火柴盒的形状是长方体(d) 压路机的形状是圆柱体(e) 甜丸子的形状是球体
$(a)$ 两条线段全等，如果长度相同。$(b)$ 在两个全等角中，一个角的度数为 $70^{\circ}$；另一个角的度数是 $70^{\circ}$。$(c)$ 当我们写 $\angle A = \angle B$ 时，我们实际上是指 $m\angle A=m\angle B$。
已知：根据对应关系 $ABC\Leftrightarrow FED$，$\triangle ABC \cong \triangle FED$。需要：写出三角形的所有对应全等部分。解答：如已知 $\Delta ABC\cong\Delta FED$。让我们画出 $\triangle ABC$ 和 $\triangle FED$。三角形的对应全等部分用 "$\Leftrightarrow$" 表示，从图中我们可以写出 $\triangle ABC$ 和 $FED$ 的对应部分。给定三角形 $\triangle ABC$ 和 $\triangle FED$ 的对应角：$\angle A\Leftrightarrow\angle F$ $\angle B\Leftrightarrow\angle E$ $\angle C\Leftrightarrow\angle D$ 给定三角形 $\triangle ABC$ 和 $\triangle FED$ 的对应边：$\overline{AB}\Leftrightarrow\overline{FE}$ $\overline{BC}\Leftrightarrow\overline{ED}$ $\overline{AC}\Leftrightarrow\overline{FD}$ 阅读更多
"
需要：我们需要画一个正八边形的草图，并通过连接八边形的恰好四个顶点来画一个矩形。解答：如图所示，通过连接八边形的恰好四个顶点，我们可以得到一个矩形。