数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
已知：拉贾斯坦邦人口为 570 लाख，北方邦人口为 160 लाख。拉贾斯坦邦面积为 3 लाख平方公里，北方邦面积为 2 लाख平方公里。要求：i) 这两个邦每平方公里有多少人？ii) 哪个邦人口较少？解答：$(i)$拉贾斯坦邦人口 = 570 लाख拉贾斯坦邦面积 = 3 लाख平方公里拉贾斯坦邦每平方公里人口 = $\frac{570}{3}$ = 190/平方公里北方邦人口 = 1660 लाख北方邦面积 = 2 लाख平方公里北方邦每平方公里人口 = $\frac{1660}{2}$ = 830/平方公里$(ii)$由于…… 阅读更多
已知： $(a).\ \frac{1}{8}$ $(b).\ \frac{3}{40}$ $(c).\ \frac{3}{40}$ $(d).\ \frac{2}{7}$要求：将给定的分数转换为百分数。解答：$(a).\ \frac{1}{8}$$=\frac{1}{8}\times100$ %$=\frac{25}{2}$ %$=12.5$ %$(b).\ \frac{5}{4}$$=\frac{5}{4}\times100$ %$=5\times25$ %$=125$ %$(c).\ \frac{3}{40}=\frac{3}{40}\times100$ %$=\frac{3}{2}\times5$ %$=\frac{15}{2}$ %$=7.5$ %$(d).\ \frac{2}{7}=\frac{2}{7}\times100$ %$=\frac{200}{7}$ %$=28\ \frac{4}{7}$ %
已知： $(a).\ 0.65$ $(b).\ 2.1$ $(c).\ 0.02$ $(d).\ 12.35$要求：将给定的十进制小数转换为百分数。解答：$(a).\ 0.65=\frac{65}{100}\times100\%=65$ %$(b).\ 2.1=\frac{21}{10}\times100\%=210$ %$(c).\ 0.02=\frac{2}{100}\times100\%=2$ %(d) $12.35=\frac{1235}{100}\times100\%=1235$ %
"
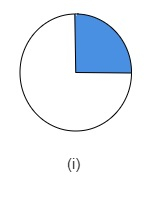
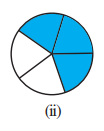
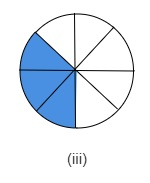
$(i)$ 彩色部分 $=\frac{1}{4}$$\therefore$ 彩色部分的百分比 $=\frac{1}{4}\times100$ % $=25$ % $(ii)$ 彩色部分 $=\frac{3}{5}$$\therefore$ 彩色部分的百分比 $=\frac{3}{5}\times100$ %$=60$ % $(iii)$ 彩色部分 $=\frac{3}{8}$$\therefore$ 彩色部分的百分比$=\frac{3}{8}\times100$ %$=\frac{3}{2}\times25$ % $=37.5$ %
不对，因为两个具有相等对应角的三角形不一定全等。在这种对应关系中，其中一个可能是另一个的放大版本。例如：这里有两个三角形 $∆ABC$，其中 $\angle A=30^{\circ},\ \angle B=40^{\circ}$ 和 $\angle C=110^{\circ}$以及 $∆PQR$，$\angle P=30^{\circ},\ \angle Q=40^{\circ}$ 和 $\angle R=110^{\circ}$但 $∆ABC$ 和 $∆PQR$ 这两个三角形不全等，即使它们具有如以下图形所示的相等角
"
已知：给定两个全等三角形。并给出它们的对应部分。要求：写出 $∆RAT≅?$解答：在给定的图形中，对应三角形和全等。$A\Leftrightarrow O$，$R\Leftrightarrow W$，$T\Leftrightarrow N$，因此我们可以写出，$\Delta RAT\cong\Delta WON$ [SAS 全等]
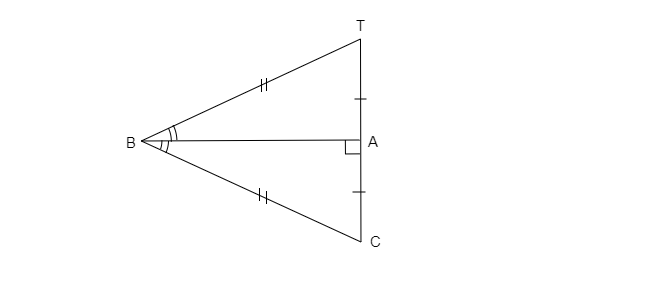
在 $\Delta BAT$ & $\Delta ABC$ 中，给定的三角形全等；$B\Leftrightarrow B$$A\Leftrightarrow A$$T\Leftrightarrow C$ [根据 SSS 全等]在 $\Delta QRS$ 和 $\Delta QPT$ 中，$PQ=RS$ [已知]$∠R=∠P$ [已知]$QR=PT$ [已知]因此，$\Delta QRS ≅ \Delta TPQ$ [根据 SAS 规则]
要求：画出两个面积相等的三角形，使得$(i)$。三角形全等。$(ii)$。三角形不全等。比较两个三角形的周长，如果它们全等和不全等。解答：$(i)$。如果两个三角形全等，则三角形的所有对应部分都将相等。让我们考虑两个三角形，$ΔABC$ 和 $ΔDEF$在给定的方格纸上，我们画了两个全等三角形。使得，$∆ ABC ≅ ∆ DEF$在方格纸上，画出两个面积相等的三角形，使得 (i) 三角形全等 (ii) 三角形不全等 你能说些什么…… 阅读更多
"
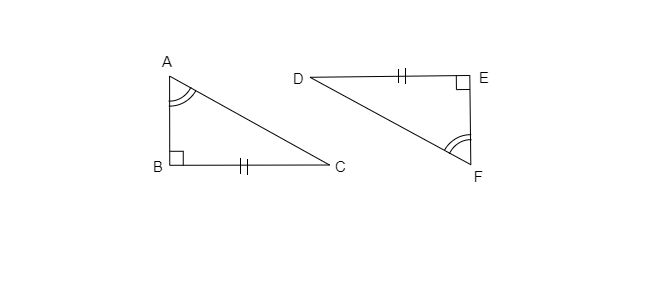
已知：两个三角形 $∆ABC$ 和 $∆FED$。要求：解释 $∆ABC ≅ ∆FED$。解答：已知 $\angle A\cong\angle F$$BC=ED$$\angle B=\angle E$在 $\triangle ABC$ 和 $\triangle FED$ 中$\angle B=\angle E=90^{\circ}$$\angle A=\angle F$$BC=ED$因此，$\triangle ABC\cong\triangle FED$ [RHS 全等准则]
"
已知：∆ABC 和 ∆PQR 在给定图形中全等。要求：命名一对额外的对应部分。解答：在 $\triangle ABC$ 和 $\triangle PQR$ 中$\angle B=\angle Q=90^{\circ}$$\angle C=\angle R$ [已知]$\overline{BC}=\overline{QR}$ [已知]因此，$\triangle ABC\cong\triangle PQR$ [ASA 全等]