数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
已知：4 个人可以在 4 天内做 4 个橱柜。要求：求 14 个人可以在 14 天内做多少个橱柜。解题方法：在这种类型的题目中，我们采用单一法。因此，4 个人在 4 天内做的橱柜数量 $=4$。1 个人在 4 天内做的橱柜数量 $=\frac{4}{4}=1$1 个人在 1 天内做的橱柜数量 $=\frac{1}{4}$14 个人在 1 天内做的橱柜数量 $=14\times\frac{1}{4}=\frac{7}{2}$。14 个人在 14 天内做的橱柜数量 $=14\times\frac{7}{2}=7\times7=49$。因此，14 个人可以在 14 天内做 49 个橱柜。
给定：六年级男女生比例为 2：3。男生总数为 24。求：我们必须求出女生数量。解法：令女生数量为 x。因此，2:3=24:x 23=24x x=24×32 x=12×3 x=36因此，六年级共有女生 36 名。
给定：给定数字为： (i) 81(ii) 272求：我们必须求出给定数字的平方的个位数。解法：我们知道，任何数字平方的个位数将是其末位数字平方的个位数。因此，(i) 81 的平方的个位数 $=$ 1 的平方的个位数1^2=1。因此，(81)^2 的个位数为 1。(ii) 272 的平方的个位数 $=$ 2 的平方的个位数2^2=4。因此，(272)^2 的个位数为 4。
下表显示了每位玩家在四场比赛中获得的分数
| 玩家 | 比赛 1 | 比赛 2 | 比赛 3 | 比赛 4 |
| A | 14 | 16 | 10 | 10 |
| B | 0 | 8 | 6 | 4 |
| C | 8 | 11 | 未参加 | 13 |
(ii) 求 C 每个比赛的平均得分
(i) A 每个比赛的平均得分为=A 在所有比赛中获得的总分在 A 参加的比赛场次中求得分除以该分数$= \frac{A\ 在所有比赛中获得的总分}{A\ 参加的比赛场次} \\dfrac{14+16+10+10}{4} \\dfrac{50}{4} \\ =12.5 (ii) 每个比赛获得的平均分数=玩家在所有比赛中获得的总分要除以玩家参加的比赛场次C 只参加了 3 场比赛。因此，我们必须除以 3 而不是 4。C 每个比赛的平均得分$= \frac{C\ 在所有比赛中获得的总分}{C\ 参加的比赛场次} \\dfrac{8+11+13}{3} \\dfrac{32}{3} \\ =10.33...(iii) B 每个比赛的平均得分$= \frac{B\ 在所有比赛中获得的总分}{B\ 参加的比赛场次} \\dfrac{0+8+6+4}{4} \\dfrac{18}{4} \\ =4.5 (iv) 比较 ... 更多
给定：3k×k=64。求：我们必须求出 k 的值。解法： 3k×k=643k^2=64k^2=643k^2=(64)3 root k=83(在两边取平方根)k=8√3k 的值为 8√3。
给定：1.6=y/1.5。求：我们必须求出 y 的值。解法： 1.6=y/1.5y=1.6×1.5y=2.40y 的值为 2.4。
已知：\( 0.007+8.5+30.08 \)求解： 我们必须找出给定的和。解答： $0.007$ $+8.500 $$+30.080$------------- $38.587$-------------因此，$0.007+8.5+30.08=38.587$。
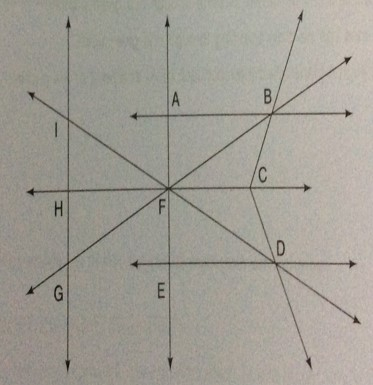
求解： 我们必须找出给定图形中的平行线条数。解答： 平行线： 在几何中，平行线可以定义为同一平面上的两条线，它们之间的距离相等，并且永远不会相交。平行线用两条名称之间的垂直线表示，例如 AB | | CD。因此，在给定的图形中，$IG \parallel AE$，$AB \parallel CH$，$CH \parallel DE$ 和 $AB \parallel DE$。给定图形中共有 4 对平行线。
(a) 我们食物的重要组成部分，也是我们周围大多数燃料的重要组成部分的非金属 A 是碳 (C)。当一个碳原子与一个氧原子结合时，形成一氧化碳 (CO)，这是一种有毒气体。当一个碳原子与两个氧原子结合时，形成二氧化碳 (CO2)，这会导致全球变暖。 因此， A 是碳 (C)；B 是一氧化碳 (CO)；C 是二氧化碳 (CO2)。(b) 元素 A（碳）属于元素周期表的第 14 组。(c) 硅 (Si) 是另一个属于同一第 14 组的元素 ... 阅读更多