数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
已知：一个湖泊中荷花的总数以这样的方式增长：它们的数目每天增加到前一天的两倍。第五天有 255 朵荷花。要求：我们必须找到第七天荷花的总数。解答：根据题意，如果第一天有 $x$ 朵荷花，那么第 $n$ 天的荷花数量$=2^{n-1}x$。设第一天荷花数量为 $x$。第五天的荷花数量$=2^{5-1}x$$2^4x=255$$x=\frac{255}{16}$第七天的荷花数量$=2^{7-1}x$$=2^6\times\frac{255}{16}$$=64\times\frac{255}{16}$$=4\times255$$=1020$第七天有 1020 朵荷花。阅读更多
已知：(i) \( \frac{-3}{5} \div 2 \)(ii) \( \frac{-2}{13} \div \frac{1}{7} \)要求：我们必须计算给定的表达式。解答：我们知道，$\frac{a}{b} \div \frac{c}{d}=\frac{a}{b}\times\frac{d}{c}$因此，(i) $\frac{-3}{5} \div 2=\frac{-3}{5} \div \frac{2}{1}$$=\frac{-3}{5}\times\frac{1}{2}$$=\frac{-3\times1}{5\times2}$$=\frac{-3}{10}$。(ii) $\frac{-2}{13} \div \frac{1}{7}=\frac{-2}{13}\times\frac{7}{1}$$=\frac{-2\times7}{13\times1}$$=\frac{-14}{13}$。
已知：两个全等圆。要求：我们必须证明全等圆的相等弦在圆心处所对的角相等。解答：考虑两个圆，其中 \( \mathrm{AB} \) 是 \( \mathrm{C}_{1} \) 的弦，( \mathrm{PQ} \) 是 \( \mathrm{C}_{2} \) 的弦。\( A B=P Q \)我们必须证明 \( \angle \mathrm{AOB}=\angle \mathrm{PXQ} \)。在 $\triangle AOB$ 和 $\triangle PXQ$中\( \mathrm{AO}=\mathrm{PX} \quad \) (全等圆的半径相等)\( BO=QX \) (全等圆的半径相等)\( AB=PQ \) (已知)因此，根据 SSS 全等，\( \Delta \mathrm{AOB} \cong \Delta \mathrm{PXQ} \) 这意味着，... 阅读更多
已知：任何正整数的平方都具有 $5p$，$5p\ +\ 1$，$5p\ +\ 4$ 的形式。要求：我们必须证明任何正整数的平方都具有 $5p$，$5p\ +\ 1$，$5p\ +\ 4$ 的形式。解答：设 'a' 为一个整数，使得 $a\ =\ 5m\ +\ r$。根据欧几里得除法算法：$a\ =\ bm\ +\ r$，其中 $0\ \underline{< }\ r\
已知：(i) 从 $\frac{-1}{1012}$ 中减去 $\frac{10}{1012}$(ii) 从 $\frac{-13}{26}$ 中减去 $\frac{-86}{13}$要求：我们必须减去给定的有理数。解答：(i) $\frac{-1}{1012}-\frac{10}{1012}=\frac{-1-10}{1012}$$=\frac{-11}{1012}$(ii) $\frac{-13}{26}-\frac{-86}{13}=\frac{-13\times1-(-86)\times2}{26}$ (13 和 26 的最小公倍数是 26)$=\frac{-13+176}{26}$$=\frac{163}{26}$。因此，$\frac{-1}{1012}-\frac{10}{1012}=\frac{-11}{1012}$ 和$\frac{-13}{26}-\frac{-86}{13}=\frac{163}{26}$。
已知：两条线段 \( A B \) 和 \( P Q \) 是全等的。\( A B=6.5 \mathrm{~cm} \)要求：我们必须找到 $PQ$ 的长度。解答：如果两条线段的长度相同，则它们是全等的。因此，$PQ=AB=6.5 \ cm$ $PQ$ 的长度是 $6.5\ cm$。
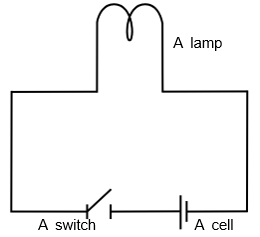
"\正确答案是选项 (b) 不完整电路。图中给出的电路类型称为不完整电路或开路，因为开关未连接。解释不完整电路也称为开路，表示电路在某处断开或断裂，不允许电流或电子流动以完成电路。在上图中，开关处于打开状态或未连接，因此电路不完整，连接到此电路的灯泡不会发光。
已知：$x:6::1:3$要求：我们必须找到 $x$ 的值。解答：我们知道，$a:b::c:d$ 意味着 $\frac{a}{b}=\frac{c}{d}$因此，$x:6::1:3$$\Rightarrow \frac{x}{6}=\frac{1}{3}$$\Rightarrow 3\times x=6\times1$$\Rightarrow 3x=6$$\Rightarrow x=\frac{6}{3}$$\Rightarrow x=2$$x$ 的值为 $2$。
已知：圆的两条弦与其交点的直径等倾斜。要求：我们必须证明这两条弦相等。解答：$AB$ 和 $AC$ 是两条弦，它们与以 $O$ 为圆心、$AD$ 为直径的圆的直径等倾斜。作 $OL \perp AB$ 和 $OM \perp AC$。在 $\triangle OLA$ 和 $\triangle OMA$ 中，$\angle OLA=\angle OMA=90^o$ $OA=OA$ (公共边)$\angle LAO=\angle MAO$ (已知)因此，\( \triangle \mathrm{OLA} \cong \triangle \mathrm{OMA} \) (根据 AAS 全等)\( \Rightarrow \mathrm{OL}=\mathrm{OM} \) (全等三角形对应边相等)这意味着，弦与圆心 $O$ 的距离相等。\( \Rightarrow AB=AC \) (圆中距离圆心相等的弦相等)... 阅读更多
已知：\( \left(\frac{a}{b}\right)=\left(\frac{5}{2}\right)^{-3} \times\left(\frac{8}{15}\right)^{-3} \)要求：我们必须找到 \( \left(\frac{a}{b}\right)^{-2} \)。解答：我们知道，$a^m \times b^m=(a\times b)^m$$\frac{a}{b}=(\frac{5}{2})^{-3} \times(\frac{8}{15})^{-3}$$=(\frac{5}{2}\times\frac{8}{15})^{-3}$$=(\frac{4}{3})^{-3}$$(\frac{a}{b})^{-2}=[(\frac{4}{3})^{-3}]^{-2}$$=(\frac{4}{3})^{-3\times-2}$$=(\frac{4}{3})^{6}$因此，$(\frac{a}{b})^{-2}=(\frac{4}{3})^{6}$。