平均速度和平均速率

---

引言

平均速度和平均速率是运动学中的两个重要概念。物体所走距离与所用时间的比值称为速度。

速率是物体位移与所用时间的比值。速度是标量。速率是矢量。必须知道大小和方向才能将速率定义为矢量。速度和速率的区别在于，速率是有方向的速度。例如，一辆自行车以50公里/小时的速度行驶表示其速度。一辆自行车以50公里/小时的速度向东行驶表示其速率。

$$\mathrm{速度= s=\frac{距离}{时间}}$$

$$\mathrm{速率= v=\frac{位移}{时间}}$$

总路程与总时间的比值称为平均速度。距离定义为物体位置的变化。但在特定方向上，位置变化称为位移。在相等的时间段内，物体覆盖的距离不相等，则其速率被称为可变的。但在相等的时间段内，物体覆盖的距离相等，则其速率被称为均匀的。

什么是平均速率？

位移变化与位移发生时的时间间隔的比值称为平均速率。位移的符号决定平均速率是正数还是负数。米每秒是平均速率的SI单位。表示为ms^-1。它也是一个矢量。位移变化表示为Δx，时间间隔表示为Δt。

$$\mathrm{平均速率= \overrightarrow{v}=\frac{\Delta x}{\Delta t}m/s}$$

如何求平均速率？

求平均速率的公式为：

平均速率 $\mathrm{\overrightarrow{v}=\frac{\Delta x}{\Delta t}m/s}$

位移变化

$$\mathrm{\Delta x=x_f-x_i}$$

$$\mathrm{x_i -初始位移}$$

$$\mathrm{x_f-最终位移}$$

时间间隔

$$\mathrm{\Delta t=t_f-t_i}$$

$$\mathrm{t_i-结束时间}$$

$$\mathrm{t_f-开始时间}$$

因此

$$\mathrm{\overrightarrow{v}=\frac{\Delta x}{\Delta t}=\frac{x_f-x_i}{t_f-t_i}}$$

$$\mathrm{\Delta x-位移变化}$$

$$\mathrm{\Delta t-总时间}$$

$$\mathrm{\overrightarrow{v}-平均速率}$$

平均速率示例

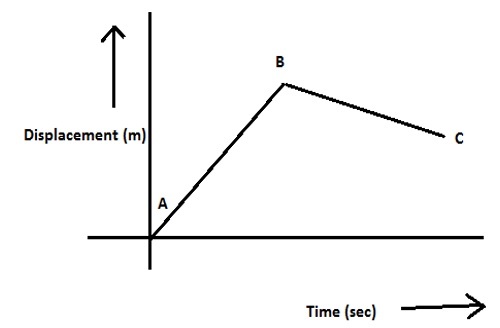
在图像中，物体从A移动到B是初始位移，然后从B移动到C是最终位移。X轴和Y轴分别表示位移和时间。起始时间为零。设初始位移为45.4米，最终位移为36米。物体总共花费4秒。

当起始时间为零时，平均速率为

$$\mathrm{\overrightarrow{v}=\frac{\Delta x}{t}}$$

$$\mathrm{\Delta x=x_f-x_i}$$

给定数据

$$\mathrm{x_f=36\:m}$$

$$\mathrm{x_i=45.4\:m}$$

$$\mathrm{t=4\:sec}$$

$$\mathrm{\overrightarrow{v}=\frac{36-45.4}{4}=-\frac{9.4}{4}=-2.35\:ms^{−1}}$$

平均速率为-2.35m/s。我们已经知道，位移的符号决定平均速率是正数还是负数。此处位移的符号为负数，因此平均速度值也为负数。

平均速度和平均速率的区别

平均速度	平均速率
总路程与总时间的比值称为平均速度。	位移变化与位移发生时的时间间隔的比值称为平均速率。
平均速度没有特定方向。因此，它是标量。	平均速率总是取决于方向。因此，它是矢量。
平均速度始终为正。	平均速率可以为正或负。因为平均速率取决于方向和位移。
平均速度 $\mathrm{S=d/t\:ms^{−1}}$	平均速率 $\mathrm{\overrightarrow{v}=\frac{\Delta x}{\Delta t}m/s}$
示例：一辆自行车以40公里/小时的速度行驶。	一辆自行车以40公里/小时的速度向南行驶。

表1：平均速度和平均速率的区别

平均速率何时为零？

当物体在位移后试图返回起始位置或物体处于静止点时，平均速率为零。换句话说，如果物体的位移为零，则平均速率变为零。例如，一辆汽车从A点行驶到B点，然后返回A点。在这种情况下，可以计算汽车的速度，但不能计算速率，因为位移为零。但如果一辆汽车从A点行驶到B点并在B点停止。在这种情况下，可以计算位移。因此，在这种情况下，平均速率没有变为零的可能性。

结论

速度定义为粒子位置变化的比率。在特定方向上发生粒子的位置变化比率称为速率。总路程与总时间的比值称为平均速度。位移变化与位移发生时的时间间隔的比值称为平均速率。角速度也定义为角位移变化的差值。角速度随时间的变化率定义为角加速度。如果物体的位移为零，则平均速率变为零。平均速度和平均速率的SI单位为米每秒$\mathrm{(ms^{−1})}$。

常见问题

Q1. 一列长200米火车通过一座长800米的桥梁。当它以36公里/小时的均匀速度行驶时，求它穿过桥梁所需的时间。

答：已知

$$\mathrm{速度=36\:km/h}$$

$$\mathrm{v=\frac{36×1000}{3600}=10\:m/s}$$

总距离 $\mathrm{=d=200+800=1000\:m}$

$$\mathrm{速度\:v=\frac{d}{t}}$$

$$\mathrm{t=\frac{d}{v}\:sec}$$

穿过桥梁所需的时间 $\mathrm{=\frac{1000}{10}=100\:sec}$

Q2. 定义标量和矢量。

答：具有大小但没有方向的物理量称为标量。速度、时间、体积、温度、距离和密度是标量的例子。既有大小又有方向的量称为矢量。速率、角速度、力、电场、线性动量和偏振是矢量的例子。矢量的大小称为矢量的模。

Q3. 什么是角速度？

答：物体的角速度定义为它每秒绕旋转轴旋转的角度。它是一个矢量。角速度是物体在时间t内所成的角度。

角速度 = $\mathrm{ω=\frac{\theta}{t}\:rad/sec}$

这里

θ=物体所成的角度

t=时间

Q4. 加速度和速度之间有什么关系？

答：物体速度变化与时间的比值称为加速度。它是一个矢量，因为它既有大小又有方向。

$$\mathrm{加速度,\:a=\frac{v_f-v_i}{t}}$$

$\mathrm{v_f}$ =最终速度

$\mathrm{v_i}$ =初始速度

t=时间（秒）

Q5. 一个物体用a m/s的速度行驶其行程的一半，用b m/s的速度行驶另一半。计算物体整个行程的平均速度。

答：2D是物体经过的总距离。$\mathrm{t_1}$和$\mathrm{t_2}$分别是物体在前半段和后半段所用的时间。S是平均速度。

通常，

$$\mathrm{平均速度\:S=\frac{d}{t}}$$

a是前半段的速度，b是后半段的速度。因此，从速度公式可知：

$$\mathrm{t=\frac{2D}{a}}$$

$$\mathrm{t_1=\frac{D}{a};\:t_2=\frac{D}{b}}$$

$$\mathrm{总时间\:t=t_1+t_2}$$

$$\mathrm{t=\frac{D}{a}+\frac{D}{b}=D(\frac{1}{a}+\frac{1}{b})}$$

$\mathrm{\therefore}$ 将两个t的方程等同

$$\mathrm{\frac{2D}{s}=D(\frac{1}{a}+\frac{1}{b})}$$

$$\mathrm{平均速度=S=\frac{2ab}{a+b}m/s}$$