理想滤波器（低通、高通、带通和带阻）的特性

---

什么是滤波器？

滤波器是一种频率选择性网络，即它允许某些频率的信号传输，而没有衰减或衰减非常小，并且它会抑制所有其他频率分量。

什么是理想滤波器？

理想滤波器是一种频率选择性网络，具有非常尖锐的截止特性，即它精确地传输特定指定频带的信号，并完全抑制该频带之外的频率信号。因此，理想滤波器的相位谱是线性的。

Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.

理想滤波器特性

根据频率响应特性，理想滤波器可以分为以下类型：

• 理想低通滤波器（LPF）

• 理想高通滤波器（HPF）

• 理想带通滤波器（BPF）

• 理想带阻滤波器（BRF）

• 理想全通滤波器

理想低通滤波器（LPF）

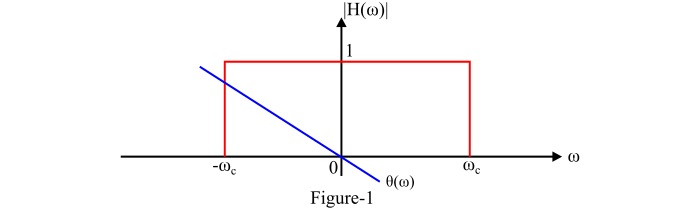
理想低通滤波器是指一种传输所有频率小于某一频率 $\mathit{\omega_{c}}$ 弧度/秒的信号，而没有任何失真，并完全阻挡所有频率高于 $\mathit{\omega_{c}}$ 弧度/秒的信号的滤波器。其中，频率 $\mathit{\omega_{c}}$ 弧度/秒称为 截止频率。理想低通滤波器的相位函数由 $[\mathit{\theta \left(\omega\right)=-\omega t_{d}}]$ 给出。

理想低通滤波器的传递函数由下式给出：

$$\mathrm{\mathit{\left | H\left(\omega\right) \right |=\left\{\begin{matrix} \mathrm{1}\:\:\mathrm{当}\:\left | \omega\ \right|<\omega_{c} \ \mathrm{0} \:\:\mathrm{当}\:\left | \omega\ \right|>\omega_{c} \end{matrix}\right.}}$$

因此，理想低通滤波器的频率响应特性为门函数或矩形函数，如图 1 所示。

理想高通滤波器（HPF）

理想高通滤波器传输所有频率高于某一频率 $\mathit{\omega_{c}}$ 弧度/秒的信号，而没有任何失真，并完全阻挡所有频率低于频率 $\mathit{\omega_{c}}$ 弧度/秒的信号。这里，频率 $\mathit{\omega_{c}}$ 弧度/秒称为 截止频率。理想高通滤波器的相位函数由下式给出：

$$\mathrm{\theta (\omega )=-\omega t_{d}}$$

理想高通滤波器的传递函数由下式给出：

$$\mathrm{\mathit{\left | H\left(\omega\right) \right |=\left\{\begin{matrix} \mathrm{0}\:\:\mathrm{当}\:\left | \omega\ \right|<\omega_{c} \ \mathrm{1} \:\:\mathrm{当}\:\left | \omega\ \right|>\omega_{c} \end{matrix}\right.}}$$

图 2 显示了理想高通滤波器的频率响应特性。

理想带通滤波器（BPF）

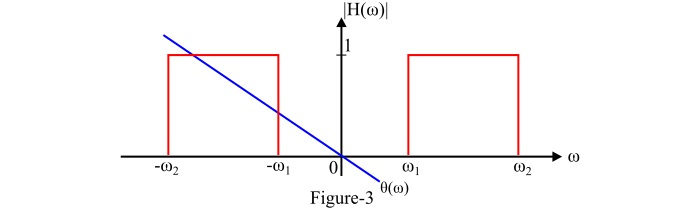
理想带通滤波器传输所有频率在某一频带 $\mathit{\left(\omega _{\mathrm{2}}-\omega_{\mathrm{1}}\right)}$ 弧度/秒内的信号，而没有任何失真，并完全阻挡该频带之外的所有频率信号。

频带 $\mathit{\left(\omega _{\mathrm{2}}-\omega_{\mathrm{1}}\right)}$ 称为 带通滤波器的带宽。

为了无失真传输，理想带通滤波器的相位函数由下式给出：

$$\mathrm{\mathit{\theta\left(\omega\right)=-\omega t_{d}}}$$

理想带通滤波器的传递函数由下式给出：

$$\mathrm{\mathit{\left | H\left(\omega\right) \right |=\left\{\begin{matrix} \mathrm{1}\:\:\mathrm{当}\:\left | \omega_{\mathrm{1}}\ \right|<\omega< \left | \omega_{2}\ \right| \\mathrm{0} \:\:\mathrm{当}\:\omega<\left | \omega_{\mathrm{1}}\ \right|\&\:\omega>\left | \omega_{\mathrm{2}}\ \right| \end{matrix}\right.}}$$

图 3 显示了理想带通滤波器 (BPF) 的频率响应特性。

理想带阻滤波器（BRF）

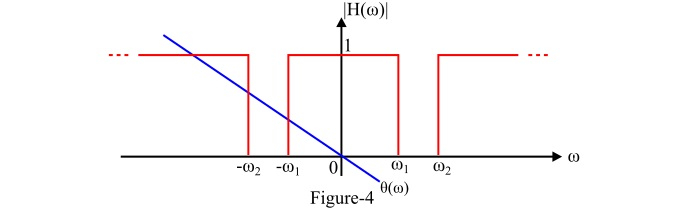
理想带阻滤波器完全抑制所有频率在某一频带 $\mathit{\left(\omega _{\mathrm{2}}-\omega_{\mathrm{1}}\right)}$ 弧度/秒内的信号，并传输该频带之外的所有频率信号，而没有任何失真。

在这种情况下，频带 $\mathit{\left(\omega _{\mathrm{2}}-\omega_{\mathrm{1}}\right)}$ 称为抑制带。带阻滤波器也称为 带阻滤波器 (BSF) 或带消除滤波器 (BEF)。 理想带阻滤波器的相位函数为 $\mathit{\theta\left(\omega\right)=-\omega t_{d}}$。

理想带阻滤波器的传递函数由下式给出：

$$\mathrm{\mathit{\left | H\left(\omega\right) \right |=\left\{\begin{matrix} \mathrm{0}\:\:\mathrm{当}\:\left | \omega_{\mathrm{1}}\ \right|<\omega< \left | \omega_{\mathrm{2}}\ \right| \\mathrm{1} \:\:\mathrm{当}\:\omega<\left | \omega_{\mathrm{1}}\ \right|\&\:\omega>\left | \omega_{\mathrm{2}}\ \right| \end{matrix}\right.}}$$

图 4 显示了理想带阻滤波器的频率响应特性。

理想全通滤波器

全通滤波器是一种频率选择性网络，它传输所有频率的信号，而没有任何失真。也就是说，全通滤波器的带宽是无限的，如图 5 所示。理想全通滤波器的传递函数由下式给出：

$$\mathrm{\mathit{\left| H\left(\omega\right)\right |=\left\{\mathrm{1}\:\:\mathrm{对于所有}\:\omega\right.}}$$

理想全通滤波器为了无失真传输的相位函数为 $\mathit{\theta\left(\omega\right)=-\omega t_{d}}$。

注意 - 所有理想滤波器都是非因果系统。因此，它们都不能在物理上实现。