数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学什么是理想重建滤波器？
什么是数据重建？
数据重建定义为从采样信号$x_{\mathit{s}}\mathrm{\left ( \mathit{t}\right)}$中获得模拟信号$x\mathrm{\left(\mathit{t}\right)}$的过程。数据重建也称为插值。
采样信号由下式给出：
$$\mathrm{\mathit{x}_{\mathit{s}}\mathrm{\left ( \mathit{t}\right)}\:\mathrm{=}\:\mathit{x}\mathrm{\left(\mathit{t}\right)}\sum_{\mathit{n}=-\infty}^{\infty}\:\delta \mathrm{\left ( \mathit{t-nT} \right )}}$$
$$\mathrm{\Rightarrow \mathit{x}_{\mathit{s}}\mathrm{\left ( \mathit{t}\right)}\:\mathrm{=}\sum_{\mathit{n}=-\infty}^{\infty}\:\mathit{x}\mathrm{\left(\mathit{nT}\right )}\delta\mathrm{\left(\mathit{t-nT}\right)}}$$
其中，$\mathit{\delta}\mathrm{\left(\mathit{t-nT} \right)}$ 除了在时刻 *t = nT* 外均为零。一个假设为线性时不变的重建滤波器具有单位冲激响应 $\mathit{h\mathrm{\left({\mathit{t}}\right)}}$。重建滤波器的输出由卷积给出：
$$\mathrm{\mathit{y\mathrm{\left({\mathit{t}}\right)}}\:\mathrm{=}\:\int_{-\infty}^{\infty}\sum_{\mathit{n}=-\infty}^{\infty}\:\mathit{x}\mathrm{\left(\mathit{nT} \right )}\delta\mathrm{\left(\mathit{k-nT} \right)}\mathit{h}\mathrm{\left ( \mathit{t-k} \right )}\mathit{dk}}$$
通过重新排列积分和求和的顺序，我们得到：
$$\mathrm{\mathit{y\mathrm{\left({\mathit{t}}\right)}}\:\mathrm{=}\:\sum_{\mathit{n}=-\infty}^{\infty}\:\mathit{x}\mathrm{\left(\mathit{nT} \right )}\int_{-\infty}^{\infty}\delta\mathrm{\left(\mathit{k-nT} \right)}\mathit{h}\mathrm{\left ( \mathit{t-k} \right )}\mathit{dk}}$$
$$\mathrm{\therefore \mathit{y\mathrm{\left({\mathit{t}}\right)}}\:\mathrm{=}\:\sum_{\mathit{n}=-\infty}^{\infty}\mathit{x}\:\mathrm{\left(\mathit{nT} \right )}\mathit{h}\mathrm{\left ( \mathit{t-nT} \right )}}$$
理想重建滤波器
理想重建滤波器用于从采样信号构建平滑的模拟信号。如果信号 $x\mathrm{\left(\mathit{t}\right)}$ 以高于奈奎斯特采样率的频率进行采样，并且采样信号 $x_{\mathit{s}}\mathrm{\left ( \mathit{t}\right)}$ 然后通过一个理想重建滤波器（或理想低通滤波器），带宽大于 $\mathit{f_{m}}$（这是信号中存在的最大频率），但小于 $\mathrm{\left(\mathit{f_{s}-f_{m}}\right )}$，并且带通幅度响应为 T，则滤波器的输出为 $x\mathrm{\left(\mathit{t}\right)}$。理想重建滤波器的带宽取为 0.5 $\mathit{f_{s}}$。
因此，理想重建滤波器的传递函数由下式给出：
$$\mathrm{\mathit{H\mathrm{\left(\mathit{f}\right)}}\:\mathrm{=}\:\begin{cases} T & \text{ for } \left|f \right|<\:0.5f_{s} \ 0 & \text{ otherwise} \end{cases}}$$
理想重建滤波器的框图如图所示。(此处应插入图片)
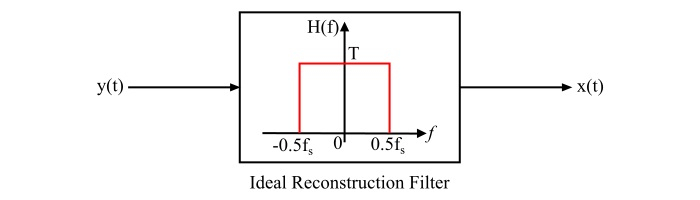
理想重建滤波器的冲激响应由下式给出：
$$\mathrm{\mathit{h}\mathrm{\left(\mathit{t}\right)}\mathrm{=}\int_{-0.5\mathit{f_{s}}}^{0.5\mathit{f_{s}}}\mathit{\mathit{T}\:e^{j\mathrm{2}\pi ft}\:df}}$$
$$\mathrm{\Rightarrow \mathit{h}\mathrm{\left(\mathit{t} \right)}\:\mathrm{=}\:\mathit{T}\mathrm{\left[\frac{\mathit{e^{j\mathrm{2}\pi ft}}}{\mathit{j}\mathrm{2}\mathit{\pi t}}\right ]^{0.5\mathit{f}_{s}}_{-0.5\mathit{f}_{s}}}\:\mathrm{=}\:\frac{\mathit{T}}{\mathit{j}\mathrm{2}\mathit{\pi t}}\mathrm{\left(\mathit{e^{j\pi f_{s}t}-e^{-j\pi f_{s}t}} \right)}}$$
$$\mathrm{\Rightarrow \mathit{h}\mathrm{\left(\mathit{t}\right)}\:\mathrm{=}\frac{1}{\mathit{\pi f_{s}t}}\mathrm{\left(\frac{\mathit{e^{j\pi f_{s}t}-e^{-j\pi f_{s}t}}}{2\mathit{j}}\right )}\:\mathrm{=}\:\frac{\mathrm{sin}\:\mathit{\pi f_{s}t}}{\mathit{\pi f_{s}t}}}$$
$$\mathrm{\therefore \mathit{h\mathrm{\left(\mathit{t}\right)}}\:\mathrm{=}\:\mathrm{sinc}\mathrm{\left(\mathit{f_{s}t}\right)}}$$
将冲激响应的值代入重建滤波器输出的表达式中，我们有：
$$\mathrm{\mathit{y\mathrm{\left({\mathit{t}}\right)}}\:\mathrm{=}\:\mathit{x\mathrm{\left({\mathit{t}}\right)}}\:\mathrm{=}\:\sum_{\mathit{n}=-\infty}^{\infty}\:\mathit{x}\mathrm{\left(\mathit{nT} \right )}\:\mathrm{sinc\:\mathit{f_{s}}}\mathrm{\left ( \mathit{t-nT} \right )}}$$
$$\mathrm{\therefore \mathit{x\mathrm{\left({\mathit{t}}\right)}}\:\mathrm{=}\:\sum_{\mathit{n}=-\infty}^{\infty}\:\mathit{x}\mathrm{\left(\mathit{nT} \right )}\:\mathrm{sinc\:\mathrm{\left ( \frac{\mathit{t}}{\mathit{T}}-\mathit{n} \right )}}}$$
因此，很明显，可以通过对以样本时间为中心的 sinc 函数对每个样本进行加权并求和来重建原始信号。理想重建滤波器是非因果的，其冲激响应不是有限的。因此，它不能用于实时应用。
3K+ 次浏览
