数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究图的补图
设'G−' 是一个简单图，其部分顶点与 'G' 的顶点相同，且如果边在 G 中不存在，则边 {U, V} 存在于 'G−' 中。这意味着，如果两个顶点在 G 中不相邻，则它们在 'G−' 中相邻。
如果存在于图 I 中的边在另一个图 II 中不存在，并且如果图 I 和图 II 组合在一起形成一个完全图，则图 I 和图 II 称为彼此的补图。
示例
在以下示例中，图 I 有两条边 'cd' 和 'bd'。它的补图 II 有四条边。
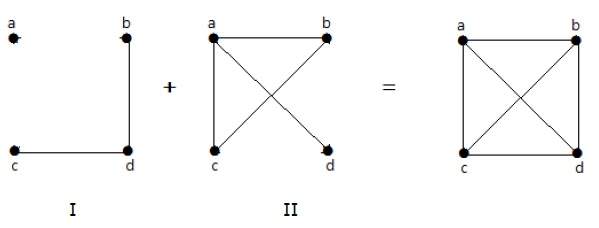
请注意，图 I 中的边不存在于图 II 中，反之亦然。因此，这两个图的组合给出了一个具有 'n' 个顶点的完全图。
注意 - 两个补图的组合构成一个完全图。
如果 'G' 是任何简单图，则
|E(G)| + |E('G-')| = |E(Kn)|，其中 n = 图中顶点的数量。
示例
设 'G' 是一个具有九个顶点和十二条边的简单图，求 'G-' 中边的数量。
你有，|E(G)| + |E('G-')| = |E(Kn)|
12 + |E('G-')| =
9(9-1)2 = 9C2
12 + |E('G-')| = 36
|E('G-')| = 24
'G' 是一个具有 40 条边和补图 'G−' 具有 38 条边的简单图。求图 G 或 'G−' 中顶点的数量。
设图中顶点的数量为 'n'。
我们有，|E(G)| + |E('G-')| = |E(Kn)|
40 + 38 = n(n-1) 2
156 = n(n-1)
13(12) = n(n-1)
n = 13
更新于： 2019年8月23日
3K+ 次浏览
广告