补码

---

二进制数系统是数字系统中最流行的数制表示技术之一。在二进制系统中，只有两个符号或可能的数字值，即 0（关）和 1（开）。由任何只有两种工作状态或可能条件的设备表示。

通常，二进制数有两种补码：一补码和二补码。要获得二进制数的一补码，只需反转给定的数字。例如，二进制数 110010 的一补码是 001101。要获得二进制数的二补码，就是给定数字的一补码加上最低有效位 (LSB) 的 1。例如，二进制数 10010 的二补码是 (01101) + 1 = 01110。

二进制数的二补码

将二进制数转换为二补码有一个简单的算法。要获得二进制数的二补码，只需反转给定的数字，然后将结果的最低有效位 (LSB) 加 1。下面给出了 4 位二补码的实现。

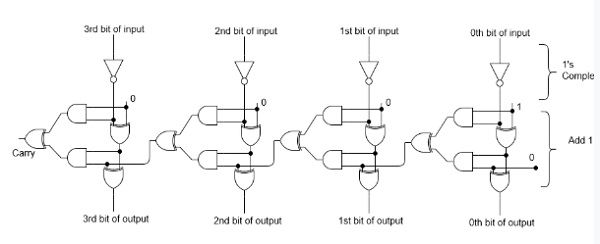
示例 1 - 查找二进制数 10101110 的二补码。

只需反转给定二进制数的每一位，结果为 01010001。然后将此结果的 LSB 加 1，即 01010001 + 1 = 01010010，这就是答案。

示例 2 - 查找二进制数 10001.001 的二补码。

只需反转给定二进制数的每一位，结果为 01110.110。然后将此结果的 LSB 加 1，即 01110.110 + 1 = 01110.111，这就是答案。

示例 3 - 查找每个 3 位二进制数的二补码。

只需反转给定二进制数的每一位，然后将这些反转后的数字的 LSB 加 1，

二进制数	一补码	二补码
000	000 (+0) 和 111 (-0)	000
001	110	111
010	101	110
011	100	101
100	011	100
101	010	011
110	001	010
111	000	001

二补码二进制数的用途

二补码二进制数有多种用途，主要用于有符号二进制数表示和二进制数的各种算术运算，例如加法、减法等。由于二补码表示是明确的，因此它在计算机数表示中非常有用。

有符号二进制数表示中的二补码

正数简单地表示为简单的二进制表示。但如果数字为负数，则使用二补码表示。首先用正号表示数字，然后取该数字的二补码。

示例 - 假设我们使用 5 位寄存器。-5 和 +5 的表示如下所示

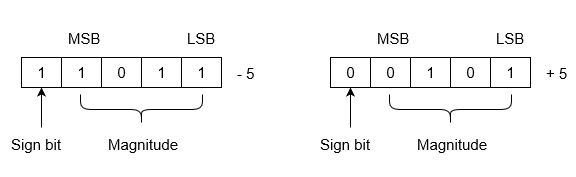
+5 的表示与符号幅值法中的表示相同。-5 使用以下步骤表示

(i) +5 = 0 0101

(ii) 取 0 0101 的二补码，即 1 1011。MSB 为 1，表示该数为负数。

负数的 MSB 始终为 1。

数字范围 - 对于 k 位寄存器，可以存储的最大正数为 (2^(k-1)-1)，可以存储的最小负数为 -(2^(k-1))。

此系统的优点是 0 只有一个表示，即 -0 和 +0。在二补码表示中，零 (0) 始终被认为是正数（符号位为 0）。因此，它是一种唯一或明确的表示。

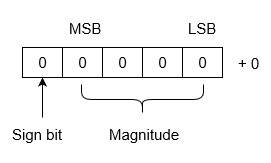
让我们看看算术运算：二补码二进制数的减法和加法。

二补码减法

使用二补码进行两个二进制数减法的算法如下所示：

• 取被减数的二补码
• 与被减数相加
• 如果上述加法的结果有进位位 1，则将其丢弃，此结果将为正数。
• 如果没有进位位 1，则取结果的二补码，这将为负数

请注意，被减数是要从另一个数（即被减数）中减去的数。

另请注意，添加“循环进位位”仅发生在一补码算术运算中，而不发生在二补码算术运算中。

示例（情况 1：当进位位为 1 时） - 计算 10101 - 00101

根据上述算法，取被减数 00101 的二补码，结果为 11011，然后将两者相加。因此，10101 + 11011 = 1 10000。由于存在进位位 1，因此丢弃此进位位 1，并取此结果为 10000，它将为正数。

示例（情况 2：当没有进位位时） - 计算 11001 - 11100

根据上述算法，取被减数 11110 的二补码，结果为 00100。然后将两者相加，因此，11001 + 00100 = 11101。由于没有进位位 1，因此取上述结果的二补码，结果为 00011，这是一个负数，即 00011，这就是答案。

同样，您可以减去两个混合（带小数部分）的二进制数。

二补码加法 -

使用二补码进行两个二进制数加法的情况有所不同。这些情况解释如下。

情况 1 - 当正数的幅度更大时，正数和负数的加法：

当正数的幅度更大时，只需取负数的二补码，并丢弃进位位 1，此结果将为正数。

示例 - 加上 1110 和 -1101。

因此，取 1101 的二补码，结果为 0011，然后与给定数字相加。因此，1110 + 0011 = 1 0001，并且进位位 1 被丢弃，此结果将为正数，即 +0001。

请注意，如果寄存器大小较大，则使用 MSB 位的符号扩展方法来保留数字的符号。

情况 2 - 当负数的幅度更大时，正数和负数的加法 -

当负数的幅度更大时，取负数的二补码，并与给定的正数相加。由于不会有任何循环进位位，因此取结果的二补码，此结果将为负数。

示例 - 在五位寄存器中添加 1010 和 -1100。

请注意，有五位寄存器，因此这些新数字将为 01010 和 -01100。现在取 01100 的二补码，结果为 10100，并添加 01010 + 10100 = 11110。然后取此结果的二补码，结果为 00010，这是一个负数，即 -00010，这就是答案。

情况 3 - 两个负数的加法 -

您需要对这两个数字取二补码，然后将这两个数字的二补码相加。由于始终存在循环进位位，因此将其丢弃。现在，也取先前结果的二补码，因此这将为负数。

或者，您可以将这两个二进制数相加，并取结果，该结果将仅为负数。

示例 - 在五位寄存器中添加 -1010 和 -0101。

这五个位数字为 -01010 和 -00101。添加这些数字的二补码，10110 + 11011 = 1 10001。由于存在进位位 1，因此将其丢弃。现在取此结果的二补码，结果为 01111，这是一个负数，即 -01111，这就是答案。

请注意，由于不存在“循环进位位”的加法，因此二补码算术运算比一补码算术运算容易得多。