数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律构建正则语言L = b + ba* 的 ∈-NFA
非确定有限自动机 (NFA) 中的 ε 转移用于在没有来自输入集 Σ 的任何符号的情况下从一个状态移动到另一个状态。
ε-NFA 以 5 元组表示定义
{Q, q0, Σ, δ, F}其中，
δ − Q × (Σ∪ε)→2Q
Q − 有限状态集
∑ − 有限输入符号集
q0 − 初始状态
F − 终结状态
δ − 转移函数
无 ε 转移的 NFA
NFA 以 5 元组表示定义
{Q, q0, Σ, δ, F}其中，
δ − Q X Σ→ 2Q
Q − 有限状态集
∑ − 有限输入符号集
q0 − 初始状态
F − 终结状态
δ − 转移函数
NFA 和带有 epsilon 的 NFA 几乎相同；唯一的区别在于它们的转移函数。
让我们考虑给定的语言 L = b+ba*
构建 ε-NFA 的步骤
步骤 1 − 下面给出了 a+ 的带 epsilon 的 NFA −
这里 a+ 表示表达式中必须至少有一个 'a'，它前面是 epsilon，后面是 epsilon。它只不过是表达式中可以有多个 'a'。
步骤 2 − 下面给出了 a* 的带 epsilon 的 NFA −
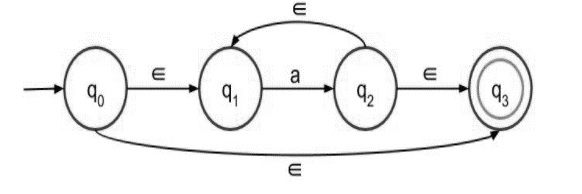
a* 表示表达式中可以有任意数量的 'a'，甚至 0（如果输入符号为空，则它也有效）。
步骤 3 − 下面给出了 (a+b) 的带 epsilon 的 NFA −
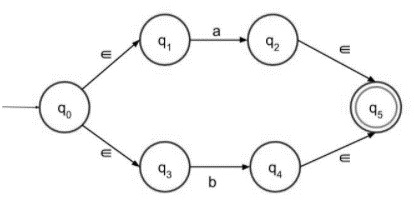
它接受 a 或 b 作为输入，两者都进入终结状态。
步骤 4 − 下面给出了 ab 的带 epsilon 的 NFA −
用 epsilon 连接 a 和 b，并且 a 必须后跟 b，然后它才能到达终结状态。
步骤 5 − 给定语言的最终带 epsilon 的 NFA 如下所示 −
L =b + ba* 分为两部分。
第一部分仅仅是 'b'，很容易构建。由于这两个术语都是用 '+' 号连接的，因此将有两个路径从第一个节点出来。第二部分需要借助构建的第二步来绘制，a* 仅仅由 b 前置。
5K+ 浏览量
