什么是带有 Epsilon 的 NFA 接受的语言？

由带有 ε 的非确定有限自动机 (NFA) 接受的语言 L，表示为 M= (Q, Σ, 𝛿, q0, F)，可以定义如下：

设 M= (Q, Σ, 𝛿, q0, F) 为一个带有 ε 的 NFA

其中，

  • Q 是状态集
  • Σ 是输入集
  • δ 是从 Q x { Σ U ε } 到 2Q 的转移函数
  • q0 是起始状态
  • F 是终结状态

NFA 接受的字符串 w 在 L 中可以表示如下：

L(M)={w| w ∈ Σ* 且 𝛿 从 q0 到 F 的 w 转移}

示例

构造一个带有 epsilon 的 NFA，它接受一个由任意数量的 a 后跟任意数量的 b 后跟任意数量的 c 组成的语言。

解决方案

这里，任意数量的 a 或 b 或 c 意味着可以有零个或多个 a 后跟零个或多个 b 后跟零个或多个 c。

因此，带有 epsilon 的 NFA 可以如下所示：

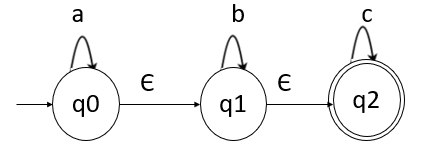
通常，epsilon 不显示在输入字符串中。

带有 epsilon 的 NFA 如下所示：

M = ({q0,q1,q2},{a,b}, 𝛿, q0,q2})

解释

  • 步骤 1 - q0 是初始状态，q0 在 'a' 上转到 q0 本身，在 epsilon 转移上 q0 转到 q1。
  • 步骤 2 - q1 在 'b' 上转到 q1 本身，在 epsilon 转移上它转到 q2。
  • 步骤 3 - q2 在 'c' 上转到 q2 本身，它是终结状态。

转移表如下所示：

状态\输入符号abCε
q0q0--q1
q1-q1-q2
q2--q2-

考虑如下所示的字符串 aabbcc：

δ(q0,aabbcc) |- δ(q0,abbcc)
             |- δ(q0,bbcc)
             |- δ(q0, εbbcc)
             |- δ(q1,bbcc)
             |- δ(q1,bcc)
             |- δ(q1,cc)
             |- δ(q1, εcc)
             |- δ(q2,cc)
             |- δ(q2,c)
             |- δ(q2, ε)

因此，在扫描完计算输入字符串后，我们到达了接受状态。

更新于：2021年6月12日

6K+ 浏览量

开启您的 职业生涯

通过完成课程获得认证

开始学习
广告