数据结构
网络
关系型数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究如何将包含 ε 转移的 NFA 转换为不包含 ε 转移的 NFA？
在这个方法中，我们尝试从给定的非确定性有限自动机 (NFA) 中移除所有 ε 转移。
该方法分步骤如下所述：
- 步骤 1 - 找出从 Q 中每个状态出发的所有 ε 转移。这将被称为 ε-闭包(qi)，其中 qi ∈ Q。
- 步骤 2 - 然后，可以获得 δ1 转移。δ1 转移表示对 δ 移动进行 ε-闭包。
- 步骤 3 - 对每个输入符号和给定 NFA 的每个状态重复步骤 2。
- 步骤 4 - 利用结果状态，可以构建不含 ε 的等效 NFA 的状态转换表。
包含 ε 的 NFA 到不包含 ε 的 NFA 如下所示：
δ1(q,a) = ∈ - closure (δ (δ∈^(q,∈𝛜),a)) 其中，δ^(q,∈𝛜) = ∈ - closure(q)
示例
将给定的包含 ε 的 NFA 转换为不包含 ε 的 NFA。
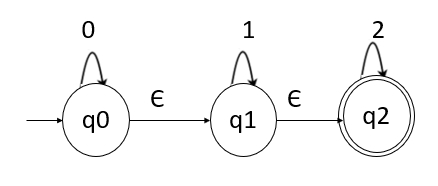
解决方案
我们首先获得每个状态的 ε-闭包，即找到从当前状态 ε 可达的状态。
因此，
- ε-closure(q0) = {q0,q1,q2}
- ε-closure(q1) = {q1,q2}
- ε-closure(q2) = {q2}
ε-closure(q0) 表示在空输入（没有输入符号）的情况下，我们可以到达 q0、q1、q2。
类似地，可以获得 q1 和 q2 的 ε-闭包。
现在，我们将获得每个状态在每个输入符号上的 δ1 转移，如下所示：
δ'(q0, 0) = ε-closure(δ(δ^(q0, ε),0))
= ε-closure(δ(ε-closure(q0),0))
= ε-closure(δ(q0,q1,q2), 0))
= ε-closure(δ(q0, 0) ∪ δ(q1, 0) U δ(q2, 0) )
= ε-closure(q0 U Φ ∪ Φ)
= ε-closure(q0)
= {q0,q1, q2}
δ'(q0, 1) = ε-closure(δ(δ^(q0, ε),1))
= ε-closure(δ(q0,q1,q2), 1))
= ε-closure(δ(q0, 1) ∪ δ(q1, 1) U δ(q2, 1) )
= ε-closure(Φ ∪q1 U Φ)
= ε-closure(q1)
= {q1, q2}
δ'(q0, 2) = ε-closure(δ(δ^(q0, ε),2))
= ε-closure(δ(q0,q1,q2), 2))
= ε-closure(δ(q0, 2) ∪ δ(q1, 2) U δ(q2, 2) )
= ε-closure(Φ U ΦU q2)
= ε-closure(q2)
= {q2}
δ'(q1, 0) = ε-closure(δ(δ^(q1, ε),0))
= ε-closure(δ(q1,q2), 0))
= ε-closure(δ(q1, 0) U δ(q2, 0) )
= ε-closure(Φ ∪ Φ)
= ε-closure(Φ)
= Φ
δ'(q1,1) = ε-closure(δ(δ^(q1, ε),1))
= ε-closure(δ(q1,q2), 1))
= ε-closure(δ(q1, 1) U δ(q2, 1) )
= ε-closure(q1 ∪ Φ)
= ε-closure(q1)
= {q1,q2}
δ'(q1, 2) = ε-closure(δ(δ^(q1, ε),2))
= ε-closure(δ(q1,q2), 2))
= ε-closure(δ(q1, 2) U δ(q2, 2) )
= ε-closure(Φ ∪ q2)
= ε-closure(q2)
= {q2}
δ'(q2, 0) = ε-closure(δ(δ^(q2, ε),0))
= ε-closure(δ(q2), 0))
= ε-closure(δ(q2, 0))
= ε-closure(Φ)
= Φ
δ'(q2, 1) = ε-closure(δ(δ^(q2, ε),1))
= ε-closure(δ(q2), 1)
= ε-closure(δ(q2, 1))
= ε-closure(Φ)
= Φ
δ'(q2, 2) = ε-closure(δ(δ^(q2, ε),))
= ε-closure(δ(q2), 2))
= ε-closure(δ(q2, 2))
= ε-closure(q2)
= {q2}现在，我们将总结所有计算出的 δ' 转移，如下所示：
δ'(q0,0)={q0,q1,q2}
δ'(q0,1)={q1,q2}
δ'(q0,2)={q2}
δ'(q1,0)= { Φ }
δ'(q1,1)={q1,q2}
δ'(q1,2)={q2}
δ'(q2,0)={ Φ }
δ'(q2,1)={ Φ }
δ'(q2,2)={q2}状态转换表如下所示：
| 状态\输入 | 0 | 1 | 2 |
|---|---|---|---|
| q0 | {q0,q1,q2} | {q1,q2} | {q2} |
| q1 | Φ | {q1,q2} | {q2} |
| q2 | Φ | Φ | {q2} |
不包含 ε 的 NFA
不包含 ε 的 NFA 如下所示：
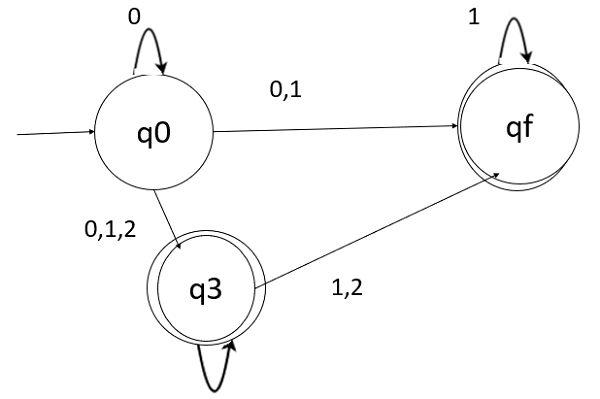
这里，q0、q1、q2 是最终状态，因为 ε-closure(q0)、ε-closure(q1) 和 ε-closure(q2) 包含最终状态 q2。
更新于： 2021年6月12日
34K+ 浏览量
广告