长方体

---

简介

在几何学中，长方体是一种立体图形或三维图形。长方体是一种具有 8 个顶点、12 条边和 6 个矩形面的凸多面体。长方体也称为矩形棱柱。现实世界中长方体的例子是矩形盒子。

什么是长方体？

想象一下，将许多全等的矩形一个叠一个地堆叠起来形成的形状。所得的形状称为长方体。

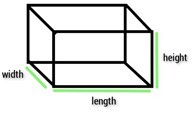
长方体的尺寸

为了描述长方体形状的边长、宽（或称深度）或高，需要强调的是，没有通用的公式。假设长方体的水平面有两个维度：长和宽，其中长是两者中较大的一个。当长方体平放在桌子上时，其高度被认为对应于任何垂直边的长度。字母“l”、“w”和“h”分别代表长方体的长、宽（或称深度）和高。长方体的边是连接两个相邻顶点的线段的一部分，其顶点是两条或多条边相交的位置，其面是其平坦的表面。

长方体的面、边和顶点

每个 3D 形状都有固定数量的面、边和顶点。长方体有六个面、十二条边和八个顶点。除了 4 个侧面外，长方体还有 2 个顶面和底面。它们都是矩形。它有 12 条边，包括 4 条连接边和顶面和底面的 8 条边。其另外 8 个顶点由顶面和底面的顶点组成。在每个顶点处，来自三个维度中的每一个的三个线段汇合在一起。

长方体的公式

请参考下表以了解基本的长方体公式。长方体有三个主要维度：l、w 和 h。

面对角线	$\mathrm{\sqrt{(l^{2}\:+\:w^{2})}\:单位}$
空间对角线	$\mathrm{\sqrt{(l^{2}\:+\:w^{2}\:+\:h^{2})}\:单位}$
周长	$\mathrm{4(l\:+\:w\:+\:h)\:单位}$

长方体的对角线

由于长方体是三维形状，因此它有两种不同类型的对角线 -

• 面对角线

• 空间对角线

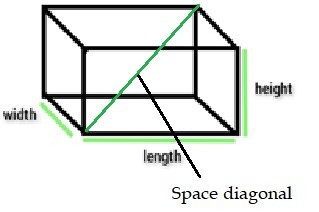
请查看下图，该图描绘了长方体的面和空间对角线。

面对角线

可以通过连接某个长方体面的相对顶点来形成面对角线，但在单个长方体面上只能形成两条对角线。由于长方体有 6 个面，因此可以画出总共 12 条面对角线。

空间对角线

连接长方体相对顶点的线段称为空间对角线。空间对角线穿过长方体的内部。因此，可以在其内部绘制 4 条空间对角线。

长方体的表面积

长方体的表面积是该形状占据的总面积。由于长方体是三维物体，因此其表面积将取决于其长、宽和高。它可能具有的两种不同类型的表面积是总表面积和侧表面积。因此，提供以下公式来确定长方体的表面积

长方体的总表面积等于 $\mathrm{S\:=\:2\:(lb\:+\:bh\:+\:lh)\:平方单位.}$

$$\mathrm{l\:=\:2h(l\:+\:b)\:平方单位是长方体侧表面积}$$

其中，

l = 长度，

b = 宽度，

h = 高度，

S = 总表面积，以及

L = 侧表面积

长方体的体积

长方体的体积用于确定它占据的空间量。长方体的长、宽和高决定了它的体积。因此，更改这些值中的任何一个都会更改形状的体积。长方体的体积以立方单位表示。因此，以下是计算长方体体积的公式 -

因此，$\mathrm{长方体的体积，V\:=\:l\times\:b\times\:h\:=\:lbh\:立方单位.}$

其中，

l = 长度

b = 宽度，以及

h = 高度

长方体的性质

长方体的关键特征使其易于识别。它们是 -

• 长方体有 6 个面、8 个顶点和 12 条边

• 长方体的顶点处仅形成直角

• 所有面的形状都是矩形。

• 可以在长方体的每个面上画两条对角线。

• 彼此相对的边平行。

• 长方体具有以下尺寸：长、宽和高。

一些现实生活中的长方体示例

我们已经编制了一些现实世界中长方体的列表。查看列表，看看您在外出时是否可以找到其中任何一个，并尝试看看您是否有自己的示例要添加

• 建筑物 - 当您在城镇或大都市周围散步时，请查看建筑物。您会注意到其中许多具有长方体的形状。

• 盒子 - 当您浏览超市、挑选一双新鞋或拆开礼物时，请注意盒子。您会发现，大多数盒子都是长方体形状的。

结论

在本教程中，我们学习了长方体以及长方体的性质。长方体是矩形棱柱。长方体的体积由 $\mathrm{l\times\:b\times\:h}$给出，侧表面积由 $\mathrm{2(l\:+\:b)\times\:h}$给出，总表面积由 $\mathrm{2(lb\:+\:bh\:+\:hl)}$给出。

常见问题

1. 尺寸为 7×6×3 单位的长方体的对角线长度是多少？

长方体公式的对角线长度为 $\mathrm{\sqrt{(l^{2}\:+\:w^{2}\:+\:h^{2})}}$ 单位。

假设长度 (l) = 7，宽度 (w) = 6，高度 (h) = 3

因此，对角线的长度等于 $\mathrm{\sqrt{(7^{2}\:+\:6^{2}\:+\:3^{2})}}$ 单位。

因此，$\mathrm{对角线的长度\:=\:\sqrt{(7^{2}\:+\:6^{2}\:+\:3^{2})}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\sqrt{(49\:+\:36\:+\:9)}\:单位\:=\:\sqrt{94}\:单位}$

2. 大卫有一个长方体盒子，尺寸为 12×7×5。盒子的体积是多少？

长方体体积 = 长度、宽度和高度，以立方单位表示。通过更改提供的变量，我们得到

$\mathrm{体积\:=\:12\times\:7\times\:5\:立方英寸}$

$\mathrm{体积\:=\:420\:立方英寸}$

3. 确定长方体的表面积。其尺寸为 8×6×4 单位？

长方体表面积的公式为 2(lw + wh + lh) 平方单位。让我们使用提供的尺寸计算长度 (l) 为 8 单位、宽度 (w) 为 6 单位和高度 (h) 为 4 单位。

因此，表面积 $\mathrm{=\:2\:\lbrace\:(8\times\:6)\:+\:(6\times\:4)\:+\:(8\times\:4)\rbrace}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:2(48\:+\:24\:+\:32)\:平方单位\:=\:2(104)\:=\:208\:平方单位.}$

4. 长方体和矩形棱柱有什么区别？

由于两者都具有 6 个矩形面、8 个顶点和 12 条边，因此长方体和矩形棱柱是相同的。此外，两者都具有盒状外观。