立方体和长方体的区别

---

介绍

立方体和长方体的区别在于，立方体有六个大小相同的正方形面，而长方体有矩形面。只有长方体和立方体是两种具有某些共同特征的立体图形，例如它们都有六个面、八个顶点和十二条边。几何学中还有许多形状，例如圆柱体、球体和圆锥体，它们具有不同的特性。此外，所有内角均为90度。

在本教程中，我们将讨论立方体和长方体的区别。

多面体

多面体是具有直边、平面、直边和锐顶点（角）的3D形状。“多面体”一词源于希腊语“poly”，意思是“许多”，而“polyhedron”则表示“区域或表面”。因此，当许多平面连接在一起时，它们就形成了一个多面体。这些形状根据它们的通常是多边形的表面命名。

根据它们的边，多面体可分为两种类型。它们是正多面体和不正多面体。

正多面体

如果正多面体的面是全等且规则的多边形，则它也被称为柏拉图立体。正多面体的所有多面角都相等。存在五种正多面体。

不正多面体

不正多面体是指具有不彼此全等的不规则多边形面以及不等的多面角的多面体。

• 欧拉公式可以表示为

$$\mathrm{F\:+\:V\:-\:E\:=\:2}$$

其中 F 表示面的数量，V 表示顶点的数量，E 表示边的数量。

立方体

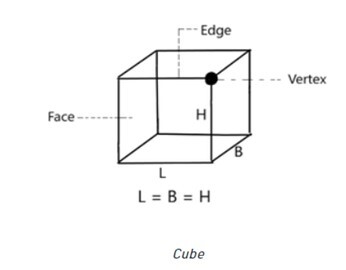
• 立方体是由大小相同的正方形面组成的三维图形。立方体的所有角都相交于900。立方体的六个相等的面都是正方形。它包含12条相同的边和8个顶点。

• 下面所示的立方体的尺寸为 l（长度）、b（宽度）和 h（高度）。立方体的边由它的长度、宽度和高度表示。三条边相交的点称为顶点。

长方体

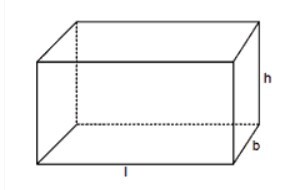
• 具有矩形面的三维图形称为长方体。长方体是一个具有盒状形状的图形。此外，长方体有8个顶点和12条边。长方体的面和边并不都相等。另一方面，长方体的相对面是相等的。

• 长方体如下图所示，其中 l 等于长度，b 等于宽度，h 等于高度，$\mathrm{l\neq\:b\neq\:h}$。

立方体和长方体的区别

立方体	长方体
高度、宽度和长度的大小都相同。侧面和边相等。	高度、宽度和距离测量值不相等。即，侧面和边不相等。
立方体的六个面都是正方形。	长方体的六个面都是矩形。
立方体的表面积测量值为1，共有12条对角线。	长方体共有12条对角线，其中3条在测量上是不同的。
示例包括魔方、骰子和冰块。	长方体的示例包括午餐盒和砖块。
立方体是正方形的三维对应物。	三维中的矩形称为长方体。
立方体的四个内部对角线的大小都应该相同。	长方体有四个内部对角线，两对内部角的测量值不同。
总表面积 $\mathrm{=\:6a^{2}}$	总表面积 $\mathrm{=\:2(lb\:+\:bh\:+\:hl)}$
曲面面积 $\mathrm{=\:4a^{2}}$	曲面面积 $\mathrm{=\:2h\:(l\:+\:b)}$
$\mathrm{体积\:=\:a^{3}}$	$\mathrm{体积\:=\:l\times\:b\times\:h}$

例题

1) 求边长为2的立方体的体积。

答案 - 我们知道立方体体积的公式是 $\mathrm{a^{3}}$

$$\mathrm{立方体体积\:=\:a^{3}}$$

$$\mathrm{=\:2^{3}\:=\:8}$$

2) 求长、宽、高分别为2、3和4的长方体的体积。

答案 - 我们知道长方体体积的公式是 $\mathrm{l\times\:b\times\:h}$

$$\mathrm{立方体体积\:=\:l\times\:b\times\:h}$$

$$\mathrm{=\:2\times\:3\times\:4}$$

$$\mathrm{=\:24}$$

3) 如果立方体的边长为4，则立方体的表面积是多少？

答案 - 给定立方体的边长为4，我们知道立方体表面积的公式是 $\mathrm{6a^{2}}$

$$\mathrm{立方体表面积\:=\:6a^{2}}$$

$$\mathrm{=\:6.4^{2}\:=\:96}$$

4) 立方体有多少个顶点（角）？

答案 - 八个。

5) 多面体能否有11个面、22个顶点和33条边？

答案 - 这可以通过欧拉公式轻松验证。

$$\mathrm{F\:+\:V\:-\:E\:=\:2}$$

给定，面(F) = 11

顶点 (V) = 22

边(E) = 33

现在将这些代入上述公式，

$$\mathrm{LHS\:=\:F\:+\:V\:-\:E}$$

$$\mathrm{=\:11\:+\:22\:-\:33\:=\:0}$$

$$\mathrm{RHS\:=\:2}$$

$\mathrm{\Longrightarrow}$ LHS 不等于 RHS

因此，对于给定条件，不存在这样的多面体。

6) 一个立体图形有14个面和12个顶点。该立体图形有多少条边？

答案 - 多面体公式/欧拉公式 $\mathrm{f\:-\:V\:-\:E\:=\:2}$

因此，$\mathrm{14\:+\:12\:-\:E\:=\:2}$

或，$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:26\:-\:E\:=\:2}$

或，$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:E\:=\:26\:-\:2\:=\:24}$

或，$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:E\:=\:24}$

因此，该立体图形有24条边

结论

立方体和长方体之间的主要区别在于，立方体有六个大小相同的正方形面，而长方体有矩形面。尽管立方体和长方体的结构相似，但根据它们的边长、对角线和面的长度，它们在某些方面有所不同。

常见问题

1. 立方体和长方体具体有什么不同？

尽管立方体和长方体的结构相当相似，但每种形状在边、长度、对角线和面的方面都存在差异。立方体有六个大小相同的正方形面，而长方体有矩形面。立方体是正方形的，而长方体是矩形的。

2. 长方体能否也称为立方体？

由于立方体是一个3D正方形物体，其所有侧面的长度、宽度和高度都相等，因此它可以被称为特殊的长方体。立方体由六个面、十二条边和八个顶点组成，每个顶点连接三个面和三条边。立方体的相对边彼此相等且平行。另一方面，长方体是一个3D矩形形状，其侧面不相等。

3. 长方体是什么形状？

长方体是一个3D图形，具有盒状形状，并有三对相对的矩形面。长方体由六个面组成，每对相对面都等于另一对。

4. 我们能把立方体称为正方形吗？

不能，正方形不能被称为立方体，因为它们的大小不同。立方体是一个3D图形，具有长度、宽度和高度，而正方形是一个2D图形，具有长度和宽度。立方体有12条边和8个顶点，而正方形有4条边和4个顶点。