ML中的DBSCAN聚类 | 基于密度的聚类

---

介绍

DBSCAN是Density-Based Spatial Clustering of Applications with Noise的缩写。它是一种无监督聚类算法。DBSCAN聚类可以处理来自海量数据中任意大小的集群，并且可以处理包含大量噪声的数据集。它基本上是基于一个区域内最小点数的标准。

什么是DBSCAN算法？

DBSCAN算法可以有效地将密集分组的点聚类到一个集群中。它可以识别大型数据集中数据点之间的局部密度。DBSCAN可以非常有效地处理异常值。与K-means算法相比，DBSCAN的一个优势是，在DBSCAN的情况下，不需要预先知道质心的数量。

DBSCAN算法依赖于两个参数：epsilon和minPoints。

Epsilon定义为每个数据点周围考虑密度的半径。

minPoints是在半径内需要的点数，以便数据点成为核心点。

该圆圈可以扩展到更高的维度。

DBSCAN算法的工作原理

在DBSCAN算法中，在每个数据点周围绘制一个半径为epsilon的圆，并将数据点分类为核心点、边界点或噪声点。如果数据点在epsilon半径内有minPoints个数据点，则将其分类为核心点。如果它拥有的点少于minPoints，则称为边界点；如果epsilon半径内没有点，则将其视为噪声点。

让我们通过一个例子来理解其工作原理。

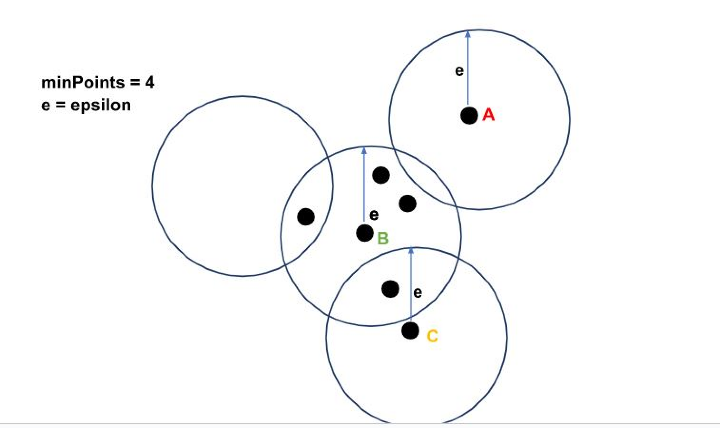
在上图中，我们可以看到点A在epsilon(e)半径内没有点。因此，它是一个噪声点。点B在epsilon e半径内有minPoints(=4)个点，因此它是一个核心点。而该点只有1个（小于minPoints）点，因此它是一个边界点。

DBSCAN算法涉及的步骤。

• 首先，找到epsilon半径内的所有点，并识别点数大于或等于minPoints的核心点。

• 接下来，对于每个核心点，如果未分配给特定集群，则为其创建一个新集群。

• 找到与核心点相关的所有密集连接的点，并将它们分配到同一个集群。如果两个点具有一个邻居点，并且该邻居点与这两个点之间的距离都在epsilon距离之内，则这两个点被称为密集连接点。

• 然后迭代数据中的所有点，并将不属于任何集群的点标记为噪声。

代码实现

## DBSCAN

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import DBSCAN
import seaborn as sns

data = pd.read_csv('/content/customers.csv')
data.rename(columns={'CustomerID':'customer_id','Gender':'gender','Age':'age','Annual Income (k$)':'income','Spending Score (1-100)':'score'},inplace=True)
features = ['age', 'income', 'score']
train_x = data[features]
cls = DBSCAN(eps=12.5, min_samples=4).fit(train_x)
datasetDBSCAN = train_x.copy()
datasetDBSCAN.loc[:,'cluster'] = cls.labels_ 
datasetDBSCAN.cluster.value_counts().to_frame()

outliers = datasetDBSCAN[datasetDBSCAN['cluster']==-1]

fig, (ax) = plt.subplots(1,2,figsize=(10,6))

sns.scatterplot(x='income', y='score',data=datasetDBSCAN[datasetDBSCAN['cluster']!=-1],hue='cluster', ax=ax[0], palette='Set3', legend='full', s=180)

sns.scatterplot(x='age', y='score',

   data=datasetDBSCAN[datasetDBSCAN['cluster']!=-1],

   hue='cluster', palette='Set3', ax=ax[1], legend='full', s=180)

ax[0].scatter(outliers['income'], outliers['score'], s=9, label='outliers', c="k")

ax[1].scatter(outliers['age'], outliers['score'], s=9, label='outliers', c="k")
ax[0].legend()
ax[1].legend()

plt.setp(ax[0].get_legend().get_texts(), fontsize='11')
plt.setp(ax[1].get_legend().get_texts(), fontsize='11')

plt.show()

输出

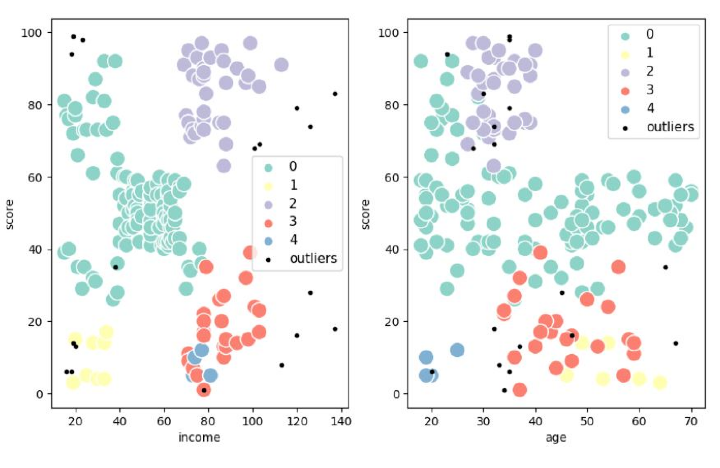
DBSCAN算法的优点

• DBSCAN不需要像K-Means算法那样预先知道质心的数量。

• 它可以找到任何形状的集群。

• 它还可以找到与任何其他组或集群不相连的集群。它可以很好地处理噪声集群。

• 它对异常值具有鲁棒性。

DBSCAN算法的缺点

• 它不适用于密度不同的数据集。

• 由于它不能被分割，因此不能与多进程一起使用。

• 如果数据集稀疏，则无法找到正确的集群。

• 它对参数epsilon和minPoints敏感

DBSCAN的应用

• 它用于卫星图像。

• 用于X射线晶体学

• 温度异常检测。

结论

DBSCAN是一种无监督聚类技术，在处理异常值和任意形状的集群时，其性能优于其他聚类算法。DBSCAN根据距离测量将密集的区域聚类在一起。它是一种空间聚类算法，也可以很好地处理噪声数据。