数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学距离公式
引言
距离公式用于计算两条线之间的距离。
在XY平面或笛卡尔平面上，连接平面上任意两点的线的长度可以通过减法确定。
坐标取决于它们在XY平面上的位置而不同。
为了找到坐标轴上两点$\mathrm{P(x_{1}\,\:y_{1})\:\&\:Q(x_{2}\,\:y_{2})}$之间的距离，我们应用距离公式。为了找到任何二维几何图形的周长或边的长度，我们使用距离公式。距离公式具有广泛的现实应用，例如船舶导航、飞机驾驶、卫星定位、任何几何位置的定位等。
在本教程中，我们将学习二维平面和三维平面中的距离公式，并附带一些已解决的示例。
坐标几何中的距离公式
XY平面上原点与坐标(𝑥1, 𝑦1) & (𝑥2, 𝑦2)之间的距离，其中𝑃 = (𝑥1, 𝑦1) & 𝑄 = (𝑥2, 𝑦2)
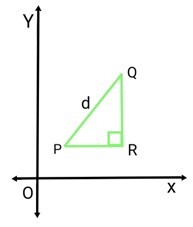
使用勾股定理，我们可以写成
$$\mathrm{PQ^{2}\:=\:PR^{2}\:+\:QR^{2}}$$
从图中可以看出，
$$\mathrm{d^{2}\:=\:(x_{2}\:-\:x_{1})^{2}\:+\:(y_{2}\:-\:y_{1})^{2}}$$
两边开平方，我们得到
$$\mathrm{d\:=\:\sqrt{(x_{2}\:-\:x_{1})^{2}\:+\:(y_{2}\:-\:y_{1})^{2}}}$$
上述表达式称为距离公式。
在二维空间中
如果𝑀(𝑎1, 𝑏1) & 𝑁(𝑎2, 𝑏2)是给定二维平面或坐标轴上的两点，则距离公式由下式给出
$$\mathrm{MN\:=\:\sqrt{(a_{2}\:-\:a_{1})^{2}\:+\:(b_{2}\:-\:b_{1})^{2}}}$$
在三维空间中
如果𝐴(𝑎1, 𝑏1, 𝑐1 ) & 𝐵(𝑎2, 𝑏2, 𝑐2)是给定三维平面上的两点，则距离公式由下式给出
$$\mathrm{AB\:=\:\sqrt{(a_{2}\:-\:a_{1})^{2}\:+\:(b_{2}\:-\:b_{1})^{2}\:+\:(c_{2}\:-\:c_{1})^{2}}}$$
已解决示例
1) 使用距离公式求两点 𝑷(𝟐, 𝟖) & 𝑸(−𝟒, 𝟏𝟔) 之间的距离。
答案 - 给定两点$\mathrm{(a_{1}\:,\:b_{1})\:=\:(2,8)\:and\:(a_{2}\:,\:b_{2})\:=\:(-4,16)}$
使用距离公式，
$$\mathrm{d\:=\:\sqrt{(x_{2}\:-\:x_{1})^{2}\:+\:(y_{2}\:-\:y_{1})^{2}}}$$
$$\mathrm{PQ\:=\:\sqrt{(-4\:-\:2)^{2}\:+\:(16\:-\:8)^{2}}}$$
$$\mathrm{PQ\:=\:\sqrt{(-6)^{2}\:+\:(8)^{2}}}$$
$$\mathrm{PQ\:=\:\sqrt{36\:+\:64}}$$
$$\mathrm{PQ\:=\:\sqrt{100}}$$
$$\mathrm{PQ\:=\:10\:单位}$$
因此，两点𝑃(2, 8) & 𝑄(−4, 16) 之间的距离为10。
2) 使用距离公式求两点 𝑿 (𝟒, −𝟕) & 𝑸 (−𝟐, 𝟏) 之间的距离。
答案 -
给定两点$\mathrm{(a_{1}\:,\:b_{1})\:=\:(4,-7)\:and\:(a_{2}\:,\:b_{2})\:=\:(-2,1)}$
使用距离公式，
$$\mathrm{d\:=\:\sqrt{(x_{2}\:-\:x_{1})^{2}\:+\:(y_{2}\:-\:y_{1})^{2}}}$$
$$\mathrm{XY\:=\:\sqrt{(-2\:-\:4)^{2}\:+\:(1\:-\:(-7))^{2}}}$$
$$\mathrm{XY\:=\:\sqrt{(-6)^{2}\:+\:(8)^{2}}}$$
$$\mathrm{XY\:=\:\sqrt{36\:+\:64}}$$
$$\mathrm{XY\:=\:\sqrt{100}}$$
$$\mathrm{XY\:=\:10\:单位}$$
因此，两点𝑋 (4, −7) & 𝑄 (−2, 1) 之间的距离为10。
3) 求两点 𝑴(𝟏, 𝟔) & 𝑵(−𝟐, 𝟑) 之间的距离？
给定两点 (𝑎1, 𝑏1) = (1, 6) 和 (𝑎2, 𝑏2) = (−2, 3)
使用距离公式，
$$\mathrm{MN\:=\:\sqrt{(a_{2}\:-\:a_{1})^{2}\:+\:(b_{2}\:-\:b_{1})^{2}}}$$
$$\mathrm{MN\:=\:\sqrt{(-2\:-\:1)^{2}\:+\:(3\:-\:6)^{2}}}$$
$$\mathrm{MN\:=\:\sqrt{(-3)^{2}\:+\:(-3)^{2}}}$$
$$\mathrm{MN\:=\:\sqrt{9\:+\:9}}$$
$$\mathrm{MN\:=\:\sqrt{18}}$$
$$\mathrm{MN\:=\:4.2426}$$
因此，两点𝑀(1, 6) & 𝑁(−2, 3) 之间的距离为4.2426。
4) 使用距离公式求三维平面上的两点 𝑷(𝟑, 𝟔, 𝟕) & 𝑸(𝟐, 𝟒, 𝟓) 之间的距离。
答案 -
给定三维平面上的两点 (𝑎1, 𝑏1, 𝑐1 ) = (3, 6, 7) 和 (𝑎2, 𝑏2, 𝑐2) = (2, 4, 5)
$$\mathrm{d\:=\:\sqrt{(a_{2}\:-\:a_{1})^{2}\:+\:(b_{2}\:-\:b_{1})^{2}\:+\:(c_{2}\:-\:c_{1})^{2}}}$$
$$\mathrm{PQ\:=\:\sqrt{(2\:-\:3)^{2}\:+\:(4\:-\:6)^{2}\:+\:(5\:-\:7)^{2}}}$$
$$\mathrm{PQ\:=\:\sqrt{(-1)^{2}\:+\:(-2)^{2}\:+\:(-2)^{2}}}$$
$$\mathrm{PQ\:=\:\sqrt{1\:+\:4\:+\:4}}$$
$$\mathrm{PQ\:=\:\sqrt{9}}$$
$$\mathrm{PQ\:=\:3}$$
因此，三维平面上两点𝑃(3, 6, 7) & 𝑄(2, 4, 5) 之间的距离为3。
5) 使用距离公式求三维平面上的两点 𝑷(𝟏, 𝟒, 𝟐) & 𝑸(𝟖, 𝟗, 𝟖) 之间的距离。
答案 -
给定三维平面上的两点 (𝑎1, 𝑏1, 𝑐1 ) = (1, 4, 2) 和 (𝑎2, 𝑏2, 𝑐2) = (8, 9, 8)。
$$\mathrm{d\:=\:\sqrt{(a_{2}\:-\:a_{1})^{2}\:+\:(b_{2}\:-\:b_{1})^{2}\:+\:(c_{2}\:-\:c_{1})^{2}}}$$
$$\mathrm{PQ\:=\:\sqrt{(8\:-\:1)^{2}\:+\:(9\:-\:4)^{2}\:+\:(8\:-\:2)^{2}}}$$
$$\mathrm{PQ\:=\:\sqrt{7^{2}\:+\:5^{2}\:+\:6^{2}}}$$
$$\mathrm{PQ\:=\:\sqrt{49\:+\:25\:+\:36}}$$
$$\mathrm{PQ\:=\:\sqrt{110}}$$
$$\mathrm{PQ\:=\:10.48808}$$
因此，三维平面上两点𝑃(1, 4, 2) & 𝑄(8, 9, 8) 之间的距离为10.48808。
6) 使用距离公式求三维平面上的两点 𝑨(𝟑, 𝟔, −𝟕) & 𝑩(𝟐, −𝟒, 𝟓) 之间的距离。
答案 -
给定三维平面上的两点 (𝑎1, 𝑏1, 𝑐1 ) = (3, 6, −7) 和 (𝑎2, 𝑏2, 𝑐2) = (2, −4, 5)。
$$\mathrm{d\:=\:\sqrt{(a_{2}\:-\:a_{1})^{2}\:+\:(b_{2}\:-\:b_{1})^{2}\:+\:(c_{2}\:-\:c_{1})^{2}}}$$
$$\mathrm{AB\:=\:\sqrt{(2\:-\:3)^{2}\:+\:(-4\:-\:6)^{2}\:+\:(5\:-\:(-7))^{2}}}$$
$$\mathrm{AB\:=\:\sqrt{(-1)^{2}\:+\:(-10)^{2}\:+\:(12)^{2}}}$$
$$\mathrm{AB\:=\:\sqrt{1\:+\:100\:+\:144}}$$
$$\mathrm{AB\:=\:\sqrt{245}}$$
$$\mathrm{AB\:=\:15.6525}$$
因此，三维平面上两点𝑃(3, 6, −7) & 𝑄(2, −4, 5) 之间的距离为15.6525。
7) 求两点 𝑰(−𝟏, −𝟏𝟐) & 𝑱(𝟒, 𝟎) 之间的距离。
答案 -
给定两点 (𝑎1, 𝑏1) = (−1, −12) 和 (𝑎2, 𝑏2) = (4, 0)
使用距离公式，
$$\mathrm{IJ\:=\:\sqrt{(a_{2}\:-\:a_{1})^{2}\:+\:(b_{2}\:-\:b_{1})^{2}}}$$
$$\mathrm{IJ\:=\:\sqrt{(4\:-\:(-1))^{2}\:+\:(0\:-\:(-12))^{2}}}$$
$$\mathrm{IJ\:=\:\sqrt{5^{2}\:+\:12^{2}}}$$
$$\mathrm{IJ\:=\:\sqrt{25\:+\:144}}$$
$$\mathrm{IJ\:=\:\sqrt{169}}$$
$$\mathrm{IJ\:=\:13}$$
因此，两点𝑀(1, 6) & 𝑁(−2, 3) 之间的距离为4.2426。
8) 使用距离公式求三维平面上的两点 𝑷(𝟑, 𝟔, 𝟕) & 𝑸(𝟐, 𝟒, 𝟓) 之间的距离。
答案 -
给定三维平面上的两点 (𝑎1, 𝑏1, 𝑐1 ) = (3, 6, 7) 和 (𝑎2, 𝑏2, 𝑐2) = (2, 4, 5)。
$$\mathrm{d\:=\:\sqrt{(a_{2}\:-\:a_{1})^{2}\:+\:(b_{2}\:-\:b_{1})^{2}\:+\:(c_{2}\:-\:c_{1})^{2}}}$$
$$\mathrm{PQ\:=\:\sqrt{(2\:-\:3)^{2}\:+\:(4\:-\:6)^{2}\:+\:(5\:-\:7)^{2}}}$$
$$\mathrm{PQ\:=\:\sqrt{(-1)^{2}\:+\:(-2)^{2}\:+\:(-2)^{2}}}$$
$$\mathrm{PQ\:=\:\sqrt{1\:+\:4\:+\:4}}$$
$$\mathrm{PQ\:=\:\sqrt{9}}$$
$$\mathrm{PQ\:=\:3}$$
因此，三维平面上两点𝑃(3, 6, 7) & 𝑄(2, 4, 5) 之间的距离为3。
距离公式建议在笛卡尔平面上找到给定两点或坐标之间的距离。
为了找到坐标轴上两点 P(x, y) 和 Q(x, y) 之间的距离，我们应用距离公式。
为了找到任何二维几何图形的周长或边的长度，我们使用距离公式。
距离公式一般而言，对于二维平面由下式给出：
三维平面的距离公式由下式给出：
$$\mathrm{d\:=\:\sqrt{(x_{2}\:-\:x_{1})^{2}\:+\:(y_{2}\:-\:y_{1})^{2}}}$$
$$\mathrm{d\:=\:\sqrt{(a_{2}\:-\:a_{1})^{2}\:+\:(b_{2}\:-\:b_{1})^{2}\:+\:(c_{2}\:-\:c_{1})^{2}}}$$
常见问题
1. 谁引入了坐标系？
坐标系，也称为笛卡尔平面，以法国数学家勒内·笛卡尔命名。
他是在坐标平面中引入几何问题求解方法的人。
他被称为坐标几何之父。
2. 什么是截距？
当直线或曲线穿过笛卡尔平面的坐标轴时，它会接触到两点，一个在水平轴上，另一个在垂直轴上。这些接触点称为平面的截距。
3. 什么是二面角？
两个平面相交时形成的角度称为二面角。相交的平面被认为是笛卡尔平面。
4. 举例说明坐标几何的一些实际应用？
为了确保飞行安全，坐标几何用于更新航班的位置。
它用于收集有关卫星位置的信息。
地球的经纬度可以用坐标系来描述。
可以用坐标几何来预测风暴的未来路径。
地图上城市和州的位置是借助坐标几何来定位的。
5. 欧几里得几何和非欧几里得几何有什么区别？
欧几里得几何处理的是二维或平面物体的研究，而非欧几里得几何处理的是曲面的研究。
6. 什么是欧几里得向量？
既具有大小又具有方向的几何对象称为欧几里得向量，或简称向量。它也称为空间向量或几何向量。这种类型的向量可以与其他向量相加。
7. 什么是坐标几何中的斜截式？
当一条直线穿过坐标轴时，它会在坐标图上与一个或两个点相交。
单位 a 从坐标图原点的距离是直线与 y 轴相交的位置。
点斜式直线方程为：$\mathrm{y\:-\:y_{1}\:=\:m(x\:-\:x_{1})}$
斜率为 m 且经过点 (0, 𝑎) 的直线方程为：
$\mathrm{y\:-\:a\:=\:m(x\:-\:0)\:其中(0,\:a)\:表示(x_{1}\:,\:y_{1})}$
因此，$\mathrm{y\:=\:mx\:+\:a}$ 是斜截式直线方程。
65 次浏览
