电力牵引：梯形速度时间曲线

干线服务的速-时曲线最好且最容易用梯形代替。图中显示了干线服务的简化梯形速-时曲线。

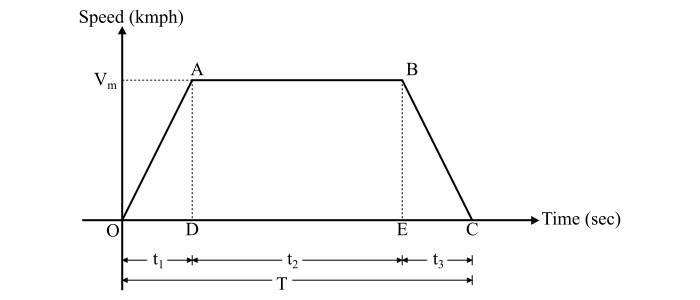
令，

• $\mathit{V_{m}}$ = 最高速度，单位为公里/小时

• $\alpha$ = 加速度，单位为公里/小时·秒

• $\beta$ = 减速度，单位为公里/小时·秒

• T = 运行总时间，单位为秒

• $\mathit{t_{\mathrm{1}}}$ = 加速时间，单位为秒

• $\mathit{t_{\mathrm{2}}}$ = 自由运行时间，单位为秒

• $\mathit{t_{\mathrm{3}}}$ = 减速时间，单位为秒

• D = 运行总距离，单位为公里

因此，加速时间（单位为秒）由下式给出：

$$\mathrm{\mathit{t_{\mathrm{1}}}\:=\:\frac{\mathit{V_{m}}}{\alpha }}$$

减速时间（单位为秒）为：

$$\mathrm{\mathit{t_{\mathrm{3}}}\:=\:\frac{\mathit{V_{m}}}{\beta }}$$

因此，自由运行时间（单位为秒）为：

$$\mathrm{\mathit{t_{\mathrm{2}}}\:=\:\mathit{T}-\mathrm{\left (\mathit{t_{\mathrm{1}}} +\mathit{t_{\mathrm{2}}} \right )}\:=\:\mathit{T}-\mathrm{\left ( \frac{\mathit{V_{m}}}{\alpha }+\frac{\mathit{V_{m}}}{\beta } \right )}}$$

现在，运行总距离（单位为公里）为：

$$\mathrm{\mathit{D}\:=\:\mathrm{加速阶段行驶距离\:+\:自由运行阶段行驶距离\:+\:制动减速阶段行驶距离}}$$

$$\mathrm{\Rightarrow \mathit{D}\:=\:\mathrm{OABC面积\:=\:AOD三角形面积\:+\:DABE矩形面积\:+\:CBE三角形面积}}$$

$$\mathrm{\Rightarrow \mathit{D}\:=\:\mathrm{\left ( \frac{1}{2}\times \mathit{V_{m}}\times \frac{\mathit{t_{\mathrm{1}}}}{3600} \right )}\:+\:\mathrm{\left ( \mathit{V_{m}}\times\frac{\mathit{t_{\mathrm{2}}}}{3600} \right )}\:+\:\mathrm{\left ( \frac{1}{2}\times \mathit{V_{m}}\times \frac{\mathit{t_{\mathrm{3}}}}{3600} \right )}}$$

代入 t₁、t₂ 和 t₃ 的值，得到：

$$\mathrm{\mathit{D}\:=\:\frac{\mathit{V_{m}^{\mathrm{2}}}}{7200\alpha}\:+\:\frac{\mathit{V_{m}} }{3600}\mathrm{\left [\mathit{T}-\mathrm{\left ( \frac{\mathit{V_{m}}}{\alpha }+\frac{\mathit{V_{m}}}{\beta } \right )} \right ]}\:+\:\frac{\mathit{V_{m}^{\mathrm{2}}}}{7200\beta }}$$

$$\mathrm{\Rightarrow \mathit{D}\:=\:\frac{\mathit{V_{m}^{\mathrm{2}}}}{7200\alpha}\:+\:\frac{\mathit{V_{m}} }{3600}\mathit{T}-\frac{\mathit{V_{m}^{\mathrm{2}}}}{3600\alpha}-\frac{\mathit{V_{m}^{\mathrm{2}}}}{3600\beta}+\frac{\mathit{V_{m}^{\mathrm{2}}}}{7200\beta}}$$

$$\mathrm{\Rightarrow \mathit{D}\:=\:\frac{\mathit{V_{m}} }{3600}\mathit{T}-\frac{\mathit{V_{m}^{\mathrm{2}}}}{7200\alpha}-\frac{\mathit{V_{m}^{\mathrm{2}}}}{7200\beta}}$$

$$\mathrm{\Rightarrow \frac{\mathit{V_{m}^{\mathrm{2}}}}{3600}\mathrm{\left ( \frac{1}{2\alpha } +\frac{1}{2\beta }\right )}-\frac{\mathit{V_{m}}}{3600}\mathit{T}\:+\:\mathit{D}\:=\:0}$$

$$\mathrm{\Rightarrow \mathit{V_{m}^{\mathrm{2}}}\mathrm{\left ( \frac{1}{2\alpha } +\frac{1}{2\beta } \right )}-\mathit{V_{m}}\mathit{T}\:+\:3600\mathit{D}\:=\:0\:\:\:\cdot \cdot \cdot \mathrm{\left ( 1 \right )}}$$

公式 (1) 是关于 $\mathit{V_{m}}$ 的二次方程

代入 $\mathrm{\left ( \frac{1}{2\alpha } +\frac{1}{2\beta } \right )}\:=\:\mathit{K}$，得到：

$$\mathrm{\mathit{KV_{m}^{\mathrm{2}}}-\mathit{V_{m}\mathit{T}}\:+\:3600\mathit{D}\:=\:0}$$

$$\mathrm{\Rightarrow \mathit{V_{m}\:=\:\frac{\mathit{T}\pm \sqrt{T^{\mathrm{2}}-\mathrm{4}\mathit{K}\times \mathrm{3600}\mathrm{D}}}{\mathrm{2}\mathit{K}}}}$$

$$\mathrm{\Rightarrow \mathit{V_{m}\:=\:\frac{\mathit{T}}{\mathrm{2}\mathit{K}}\pm \sqrt{\frac{\mathit{T^{2}}}{\mathrm{4}K^{\mathrm{2}}}-\frac{\mathrm{3600D}}{\mathit{K}}}}}$$

这里，不能采用 + 号，因为使用 + 号得到的 Vm 值远高于实际可能达到的值。因此，使用负号，得到：

$$\mathrm{\mathit{V_{m}\:=\:\frac{\mathit{T}}{\mathrm{2}\mathit{K}}- \sqrt{\frac{\mathit{T^{\mathrm{2}}}}{\mathrm{4}K^{\mathrm{2}}}-\frac{\mathrm{3600D}}{\mathit{K}}}\:\:\:\cdot \cdot \cdot \mathrm{\left ( 2 \right )}}}$$

根据公式 (2)，可以通过代入已知量的值来获得未知量。

数值示例

一列火车在水平轨道上的运行时刻表速度为 40 公里/小时，车站之间的距离为 2 公里。车站停车时间为 25 秒。假设制动减速度为 2.5 公里/小时·秒，最大速度比平均速度高 30%，如果速-时曲线近似为梯形曲线，计算运行火车所需的加速度。

解答

已知，

• 时刻表速度，$\mathit{V_{\mathit{S}}}$ = 40 公里/小时

• 车站之间的距离，D = 2 公里

$$\mathrm{\therefore \mathrm{运行时刻表时间,}\mathit{T_{S}}\:=\:\frac{\mathit{D}\times 3600}{\mathit{V_{S}}}\:=\:\frac{2\times 3600}{40}\:=\:180\:\mathrm{秒}}$$

$$\mathrm{\mathrm{实际运行时间,}\mathit{T}\:=\:\mathit{T_{S}-\mathit{T_{stop}}}\:=\:180-25\:=\:155\:\mathrm{秒}}$$

现在，

$$\mathrm{\mathrm{平均速度,}\mathit{V_{a}}\:=\:\frac{\mathit{D}\times 3600}{\mathit{T}}\:=\:\frac{2\times 3600}{155}\:=\:46.45\:\mathrm{公里/小时}}$$

$$\mathrm{\therefore \mathrm{最大速度,}\mathit{V_{m}}\:=\:1.3\mathit{V_{a}}\:=\:1.3\times 46.45\:=\:60.385\:\mathrm{公里/小时}}$$

使用公式 (1)，得到：

$$\mathrm{\mathit{V_{m}^{\mathrm{2}}}\mathrm{\left ( \frac{1}{2\alpha } +\frac{1}{2\beta}\right )}-\mathit{V_{m}T}\:+\:3600\mathit{D}\:=0}$$

$$\mathrm{\Rightarrow \frac{1}{2\alpha } +\frac{1}{2\beta}\:=\:\frac{\mathit{V_{m}T-\mathrm{3600}\mathit{D}}}{\mathit{V_{m}^{\mathrm{2}}}}}$$

$$\mathrm{\Rightarrow \frac{1}{2\alpha } +\frac{1}{2\beta}\:=\:\frac{60.385\times 155-3600\times 2 }{\mathrm{\left ( 60.385 \right )^{\mathrm{2}}}}\:=\:0.5922}$$

$$\mathrm{\Rightarrow \frac{1}{2\alpha } =0.5922-\frac{1}{2\beta}\:=\:0.5922-\frac{1}{2\times 2.5}\:=\:0.3922}$$

$$\mathrm{\therefore \alpha \:=\:\frac{1}{2\times 0.3922}\:=\:1.27\:\mathrm{公里/小时·秒}}$$

Manish Kumar Saini

更新于： 2022年5月3日

6K+ 浏览量

开启你的 职业生涯

通过完成课程获得认证

开始学习