等边三角形

---

简介

等边三角形是三条边长度都相等三角形。三角形的痕迹遍布世界各地，尤其是在建筑中。它们深受古埃及人的喜爱。根据边长的不同，三角形分为三种类型。

这些三角形分别是等腰三角形、不等边三角形和等边三角形。等边三角形是三条边和三个角都相等的三角形。由于等边三角形的每个角都是60度，因此它也被称为等角三角形。从任何顶点画出的垂直线将等边三角形的对边分成相等的长度。此外，顶角也被分成两个相等的部分，每部分与垂直线绘制点相距30度。

等边三角形

三角形的痕迹遍布世界各地，尤其是在建筑中。它们深受古埃及人的喜爱。埃及著名的金字塔的面就是三角形的。吉萨金字塔是埃及人在公元前二世纪建造的最著名的金字塔。埃及人认为金字塔的三角形形状代表着他们太阳神拉的尘世居所。

根据三角形的边长，三角形分为三种类型：等腰三角形、不等边三角形和等边三角形。等腰三角形和不等边三角形与等边三角形不同。

等边三角形是三条边和三个角都相等的三角形。由于等边三角形的每个角都是60度，因此它也被称为等角三角形。因为等边三角形的角和边都相等，所以它被认为是一个正多边形或正三角形。

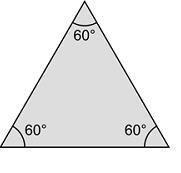
等边三角形是三条边相等的三角形，也称为正三角形。等腰三角形是等边三角形的子集，它的三条边都相等。等边三角形有3条相等的边。

不等边三角形的所有边都不相等，角也不相等。等腰三角形的两条边相等。

等边三角形的性质

等边三角形有一些性质与其他三角形不同。要识别等边三角形，可以使用下面列出的性质。

• 等边三角形是三条边都相等的三角形。

• 由于等边三角形的每个角都是60度，因此它也被称为等角三角形。

• 因为它有三条边，所以它是一个正多边形。

• 从任何顶点到等边三角形对边画出的垂直线将该边分成相等的长度。它还将顶角分成相等的两半，每半与垂直线绘制点相距30度。

• 垂心和重心位于同一位置。

• 等边三角形的中心线、角平分线和高线对于所有边都是相同的。

• 等边三角形的面积 $\mathrm{=\:\frac{\sqrt{3}a^{2}}{4}}$，其中 a = 等边三角形的边长

• 等边三角形的周长等于 3a，其中 a 是等边三角形的边长。

• 等边三角形的内角和等于180度。

等边三角形的重心

等边三角形的重心位于三角形的中心。因为所有角和边都相等，所以很容易找到重心。

我们必须从三角形的相对边上画出垂直线到每个顶点。这些垂直线必须在一个公共点相交，并且所有垂直线都必须相等，这被称为重心。

等边三角形的外心

等边三角形的外心是边上的垂直平分线的交点。外接圆穿过三角形的三个顶点。

在等边三角形中，三角形的外心与垂心、内心或重心重合。

等边三角形的面积

等边三角形的面积是它在二维平面中占据的空间。以下是计算等边三角形面积的公式

等边三角形的面积 $\mathrm{=\:\frac{\sqrt{3}a^{2}}{4}}$，其中 a = 等边三角形的边长

例题

1) 如果 PQ = QR = RP = 2 厘米，则等边三角形 PQR 的面积是多少？

答案 - 我们将使用公式 - $\mathrm{面积\:=\:\frac{\sqrt{3}}{4}\:\times\:边长^{2}}$

根据题意，边长 = 2 厘米。

因此，$\mathrm{面积\:=\:\frac{\sqrt{3}}{4}\:\times\:2^{2}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\sqrt{3}cm^{2}}$

2) 边长为 10 个单位的等边三角形的周长和半周长是多少？

答案 - 我们知道等边三角形的周长是边长的三倍，半周长是周长的一半。

边长 = 10 个单位。

因此，等边三角形的周长将是 $\mathrm{3\times\:10\:=\:30\:个单位}$

等边三角形的半周长将是 $\mathrm{\frac{30}{2}\:=\:15\:个单位。}$

3) 如果等边三角形的所有边长都是 30 英寸，则其周长是多少？

答案 - 我们知道等边三角形的周长是其边长的三倍。问题说明边长 $\mathrm{=\:30\:英寸}$

因此，等边三角形的周长是 $\mathrm{3\times\:30\:=\:90\:英寸}$

结论

三角形图案在世界各地都很常见，尤其是在建筑中。它们深受古代埃及人的喜爱。根据边长的不同，三角形可以分为三类。

这些三角形分别是等边三角形、等腰三角形和不等边三角形。等边三角形是三条边和三个角都相等的三角形。由于等边三角形的每个角都是60度，因此它也被称为等角三角形。从任何顶点画出的垂直线将等边三角形的对边分成相等的长度。此外，顶角也被分成两个相等的部分，每部分与垂直线绘制点相距30度。

常见问题

1. 如何判断一个三角形是否为等边三角形？

如果三角形的所有边都等长，则称其为等边三角形。当 X、Y 和 Z 代表三角形的三个边时，只有当 X 等于 Y 等于 Z 时，三角形才是等边三角形。如果三角形的一条边等于另一条边，则该三角形称为等腰三角形。

2. 什么类型的三角形不存在？

三角形不可能同时是钝角三角形和等边三角形。等边三角形中不存在钝角，因为所有三个角都为 60 度。

3. 是否可以形成直角等边三角形？

等边三角形永远不可能是直角三角形，因为直角三角形的一个角是 90 度，如果我们根据定义使所有角都等于 90 度，则它们的和为 270 度，这是不可能的，因为所有三角形的内角和是 180 度。

4. 三角形在你的生活中有哪些应用？

可以使用三角形建造桁架。桁架用于各种结构，包括屋顶、桥梁和建筑物。桁架是由水平梁和斜梁组合而成的三角形。桁架桥是使用桁架的桥梁。