数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究定点数和浮点数表示
数字计算机使用二进制数系统来表示计算机内部所有类型的信息。字母数字字符使用二进制位（即 0 和 1）表示。数字表示更容易设计，存储方便，精度更高。
数字表示法有多种技术，例如：二进制数系统、八进制数系统、十进制数系统和十六进制数系统等。但是，二进制数系统在数字计算机系统中表示数字最相关和流行。
存储实数
这些结构如下所示：
在现代计算中，有两种主要方法可以存储实数（即带有小数部分的数字）。它们是 (i) 定点表示法和 (ii) 浮点表示法。在定点表示法中，小数点后有固定数量的数字，而浮点数允许小数点后有可变数量的数字。
定点表示法：
这种表示法为整数部分和小数部分保留固定数量的位。例如，如果给定的定点表示法是 IIII.FFFF，则可以存储的最小值为 0000.0001，最大值为 9999.9999。定点数字表示法有三个部分：符号位、整数位和小数位。
我们可以使用以下方法表示这些数字：
- 有符号表示：范围从 -(2(k-1)-1) 到 (2(k-1)-1)，其中 k 为位数。
- 反码表示：范围从 -(2(k-1)-1) 到 (2(k-1)-1)，其中 k 为位数。
- 补码表示：范围从 -(2(k-1)) 到 (2(k-1)-1)，其中 k 为位数。
补码表示法由于其明确的属性以及更容易进行算术运算，因此在计算机系统中更受欢迎。
**示例：**假设数字使用 32 位格式，其中 1 位用于符号，15 位用于整数部分，16 位用于小数部分。
那么，-43.625 表示如下：
其中，0 用于表示 +，1 用于表示 -。000000000101011 是十进制 43 的 15 位二进制值，1010000000000000 是小数 0.625 的 16 位二进制值。
使用定点表示法的优点是性能，缺点是它们可以表示的值范围相对有限。因此，它通常不足以进行数值分析，因为它不允许足够的数字和精度。表示超过 32 位的数字必须不精确地存储。
以上是如上格式所示的 32 位表示中可以存储的最小正数和最大正数。因此，最小正数为 2-16 ≈ 0.000015（近似值），最大正数为 (215-1)+(1-2-16)=215(1-2-16) =32768，这些数字之间的差距为 2-16。
我们可以仅使用整数字段为 1 来向左或向右移动基数点。
浮点表示法：
这种表示法不会为整数部分或小数部分保留特定数量的位。相反，它为数字保留一定数量的位（称为尾数或有效数），并保留一定数量的位来说明小数点位于该数字中的哪个位置（称为指数）。
数字的浮点数表示有两个部分：第一部分表示一个有符号定点数，称为尾数。第二部分指定小数点（或二进制点）的位置，称为指数。定点尾数可以是小数或整数。浮点数始终解释为以下形式表示的数字：Mxre。
只有尾数 m 和指数 e 在寄存器中物理表示（包括它们的符号）。浮点二进制数以类似的方式表示，只是它使用以 2 为底的指数。如果尾数的最高有效位为 1，则浮点数被认为是规范化的。
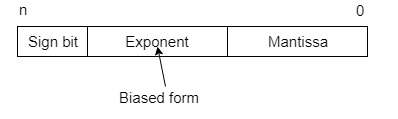
因此，实际数字为 (-1)s(1+m)x2(e-Bias)，其中 *s* 是符号位，*m* 是尾数，*e* 是指数值，*Bias* 是偏差数。
请注意，有符号整数和指数由符号表示、反码表示或补码表示表示。
浮点表示法更灵活。任何非零数都可以表示为 ±(1.b1b2b3 ...)2x2n 的规范化形式。这是数字 x 的规范化形式。
**示例：**假设数字使用 32 位格式：1 位符号位，8 位用于有符号指数，23 位用于小数部分。不存储前导位 1（因为它对于规范化数字始终为 1），它被称为“隐藏位”。
然后 -53.5 规范化为 -53.5=(-110101.1)2=(-1.101011)x25，表示如下：
其中 00000101 是指数值 +5 的 8 位二进制值。
请注意，8 位指数字段用于存储整数指数 -126 ≤ n ≤ 127。
适合 32 位的最小规范化正数为 (1.00000000000000000000000)2x2-126=2-126≈1.18x10-38，适合 32 位的最大规范化正数为 (1.11111111111111111111111)2x2127=(224-1)x2104 ≈ 3.40x1038。这些数字表示如下：
浮点格式的精度是为二进制数字保留的位置数加一（对于隐藏位）。在此处考虑的示例中，精度为 23+1=24。
1 和下一个规范化浮点数之间的差距称为机器 epsilon。对于上述示例，差距为 (1+2-23)-1=2-23，但由于非均匀间距，这与最小正浮点数相同，这与定点情况不同。
请注意，非终止二进制数可以用浮点表示法表示，例如，1/3 = (0.010101 ...)2 不能是浮点数，因为它的二进制表示是非终止的。
IEEE 浮点数表示法：
IEEE（电气和电子工程师协会）已将浮点表示法标准化为下图所示。
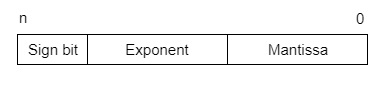
因此，实际数字为 (-1)s(1+m)x2(e-Bias)，其中 *s* 是符号位，*m* 是尾数，*e* 是指数值，*Bias* 是偏差数。符号位对于正数为 0，对于负数为 1。指数由补码表示。
根据 IEEE 754 标准，浮点数以以下方式表示：
- 半精度 (16 位)：1 个符号位、5 位指数和 10 位尾数
- 单精度 (32 位)：1 个符号位、8 位指数和 23 位尾数
- 双精度 (64 位)：1 个符号位、11 位指数和 52 位尾数
- 四精度 (128 位)：1 个符号位、15 位指数和 112 位尾数
特殊值表示：
根据 IEEE 754 标准，存在一些取决于指数和尾数的不同值的特殊值。
- 所有指数位为 0，所有尾数位为 0 表示 0。如果符号位为 0，则为 +0，否则为 -0。
- 所有指数位为 1，所有尾数位为 0 表示无穷大。如果符号位为 0，则为 +∞，否则为 -∞。
- 所有指数位为 0 且尾数位非零表示非规格化数。
- 所有指数位为1且尾数位非零表示错误。
浏览量：9.8万+
