数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会研究
时尚研究
法律研究给出一个将 NFA 转换为 DFA 的示例问题。
问题
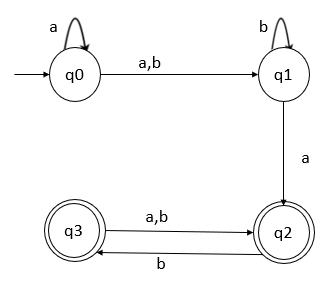
考虑一个非确定有限自动机 (NFA)，并将该 NFA 转换为等效确定有限自动机 (DFA)。
解决方案
让我们为给定的图表构建 NFA 转换表 −
| 状态\输入 | a | b |
|---|---|---|
| ->q0 | {q0,q1} | q0 |
| q1 | q2 | q1 |
| q2 | q3 | q3 |
| q3 | - | q2 |
DFA 不能有多个状态。因此，在上图中将 {q0,q1} 视为一个状态。
我们来将上面的表格转换为等效的 DFA
| 状态\输入 | a | b |
|---|---|---|
| ->q1 | [q0,q1] | q0 |
| [q0,q1] | [q0q1q2] | [q0q1] |
| *[q0q1q2] | [q0q1q2q3] | [q0q1q3] |
| *[q0q1q2q3] | [q0q1q2q3] | [q0q1q2q3] |
| *[q0q1q3] | [q0q1q2] | [q0q1q2] |
在 DFA 中，终态是 q2 和 q3，无论 q2 和 q3 出现于何处，该状态都变为终态。
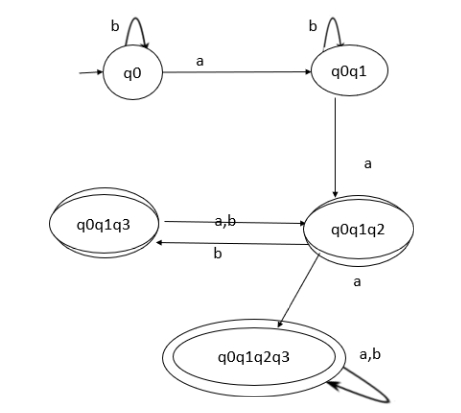
现在，DFA 的转换图如下 −
更新于： 12-6-2021
10K+ 阅读
广告