数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
法律研究数据结构中红黑树的插入
红黑树是一种自平衡二叉搜索树，其中树的每个节点都着色为红色或黑色。我们可以在红黑树上执行三种类型的操作——搜索、插入和删除。
假设我们必须在以下红黑树中插入一个元素。
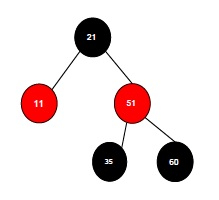
在红黑树中插入元素的想法非常简单——我们就像在普通二叉树中插入一样进行插入。我们从根节点开始，检查节点的颜色，并将其插入特定位置。但是，在红黑树中，应该有一些额外的程序来插入元素。
但是，我们应该知道，当红黑树满足以下条件时，它是平衡的：
每个根节点必须是黑色的。
每个节点要么是红色，要么是黑色。
如果一个节点是红色的，那么它的子节点必须是黑色的。
从根到末端的路径必须包含相同数量的黑色节点。
如果我们想在红黑树中插入一个新节点，那么我们可以通过查看插入步骤来实现。
在红黑树中插入元素的步骤：
检查树是否为空。如果树为空，则插入一个新节点并将其颜色设置为黑色。（因为根节点必须始终为黑色）
否则，如果树不为空，则将新节点作为叶节点插入到末尾，并将其颜色设置为红色。
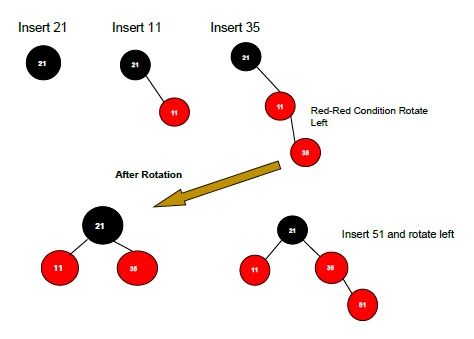
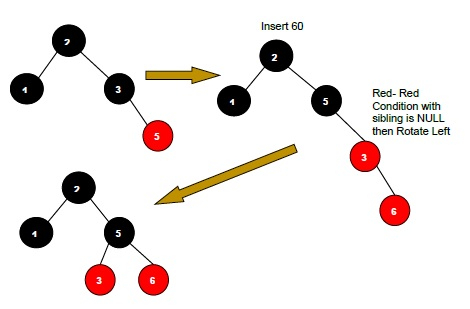
如果新节点的父节点为红色，并且其相邻（父节点的）节点也为红色，则翻转两个相邻节点和父节点以及祖父母节点（如果它不是根节点，否则只翻转父节点和相邻节点的颜色）的颜色，即黑色。
如果新节点的父节点为红色，并且其相邻（父节点的）节点为空或为 NULL，则旋转（左左或左右旋转）新节点和父节点。
有两种类型的旋转适用 - 左左旋转和左右旋转。旋转仅在某些条件下适用。条件是：
如果新节点的父节点为红色，并且相邻节点为空或为 NULL，则进行左旋转或右旋转。
在左左旋转中，翻转父节点和祖父母节点的颜色。将父节点设为祖父母节点，并将祖父母节点设为子节点。
算法
RBTreeInsertion(root,key)
//The color of the inserted new node is Red color[key] <- Red while(key≠root and color (p[key]=Red)) do if p[key]= left(p[p[key]]) Then y←right[p[p[key]] // If the parent of the new node is Red(if there is Grandparent instead root Node) Flip the color. if color[y]← Red then color(p[key])← Black color(p[p[key]])← Red key← p[p[key]] else if key← right[p[key]] then key← p[key] //When parent of new node has the red color and its sibling is NULL LeftRotate(root,key) color(p[key]) ← Black color(p[p[key]]) ← Red RotateRight(root,p[p[key]]) else exchange then left and right elements to make it balance. color(root)← Black
更新于: 2021年2月5日
7K+ 浏览量
广告