整数练习题

---

简介

• 整数是数学中最重要概念之一，其中大多数与本主题相关。您可以通过练习多个整数练习题来练习此概念。

• 在数学中，整数被描述为可能为正、负或零的数字。

• 但是，这些数字不能构成分数。

• 根据整数练习题，这些数字可以用于执行各种数学运算，包括加法、减法、乘法和除法。

• 根据整数练习题，整数的例子包括 1、2、5、8、-8、-12 和 6。在本教程中，我们将讨论整数。

整数

• 拉丁语“integer”表示“整体”或“完整”。因此，整数不包括分数和小数。

• 整数可以包含正数和负数，包括零，是一个没有小数或分数部分的数字。

• 整数包括 -5、0、1、5、8、97 和 303 等。

• Z 是所有整数的集合，包含以下内容：

正数 - 如果一个数大于零，则它被认为是正数

例如 - 1、2、3 等。

负数 是小于零的数

例如 - -1、-2、-3 等

注意 - 零被描述为既不是正数也不是负数

整数规则

对于整数，指定以下规则：

• 两个整数的和将是一个整数

• 两个整数的积将是一个整数

整数代数

整数可用于以下四种基本算术运算：

• 整数的加法

• 整数的减法

• 整数的乘法

• 整数的除法

整数的加法

整数加法规则：

加两个整数时，使用以下指南：

当两个整数符号相同时：将它们的绝对值相加，并将结果赋予与输入整数相同的符号。

当两个整数符号不同时：确定两个数的绝对值之间的差，然后将两个数中较大数的符号加到结果中。

例如，简化以下方程式 $\mathrm{1\:+\:9\:+\:11}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:给定方程式为\:1\:+\:9\:+\:11}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:21}$

整数的减法

整数减法规则：

要执行两个整数的减法，请应用以下规则

要执行两个整数的减法，请应用以下规则：

将减数的符号更改为将运算转换为加法问题。应用相同的规则来加整数并解决上述步骤中获得的问题。

例如，简化以下方程式 $\mathrm{22\:-\:10\:-\:2}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:给定方程式为\:22\:-\:10\:-\:2}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:22\:-\:12}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:10}$

整数的乘法和除法

整数乘法或除法规则：

乘或除各个整数的绝对值，结果的符号由一个简单的规则确定：如果两个整数符号相同，则结果为正，否则为负。

例如，简化以下方程式 $\mathrm{100\:\div\:(5\:\times\:4)}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:给定方程式为\:100\:\div\:(5\:\times\:4)}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:100\:\div\:20}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:5}$

数轴上的整数

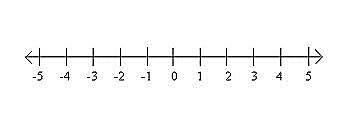
数字的直线以视觉方式显示为数轴。此线用于比较在无限线上等距间隔的整数，该无限线在两侧水平延伸。

在数轴上，可以视觉化表示正整数和负整数。数轴上整数的表示对于执行数学运算很有用。在数轴上排列整数时，请牢记以下基本注意事项：

• 正整数位于数字零的右侧，因为它们大于 0

• 负数位于零的左侧，因为它们小于 0。

• 零通常位于中间，因为它既不能是正数也不能是负数。

解题示例

示例 1 - 简化以下方程式 $\mathrm{2\:+\:8\:-\:(-5)}$

解 - 给定方程式为 $\mathrm{2\:+\:8\:-\:(-5)}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:10\:-\:(-5)}$.

我们知道两个负号的乘积得到一个正号，现在应用此规则

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:10\:+\:5}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:15}$

示例 2 - 简化以下方程式 $\mathrm{2\:\times\:(-3)\:+\:8\:(-5)}$

解 - 给定方程式为 $\mathrm{2\:\times\:(-3)\:+\:8\:(-5)}$

我们知道正负号的乘积得到一个负号，现在应用此规则

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:2\:\times\:(-3)\:+\:8\:(-5)}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:-6\:+\:8\:+\:-5}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:-3}$

示例 3 - 简化以下方程式 $\mathrm{(2\:\times\:4\:+\:8)\:\div\:4}$

解 - 给定方程式为 $\mathrm{(2\:\times\:4\:+\:8)\:\div\:4}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:(8\:+\:8)\:\div\:4}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:16\:\div\:4}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:4}$

示例 4 - 解 $\mathrm{5\:+\:9(2\:\times\:2)\:-\:4}$

解 - 给定方程式为 $\mathrm{5\:+\:9(2\:\times\:2)\:-\:4}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:5\:+\:9(4)\:-\:4}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:5\:+\:36\:-\:4}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:41\:-\:4}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:37}$

示例 5 - 解 $\mathrm{(12\:+\:14)\:\times\:16}$

解 - 给定方程式为 $\mathrm{(12\:+\:14)\:\times\:16}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:26\:\times\:16}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:416}$

示例 6 - 解 $\mathrm{(100\:\div\:20)\:+\:5}$

解 $\mathrm{=\:(100\:\div\:20)\:+\:5}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:5\:+\:5}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:10}$

示例 7 - 简化以下方程式 $\mathrm{900\:\div\:[(25\:\times\:4)\:-\:8\:-\:2]}$

解 - 给定方程式为 $\mathrm{900\:\div\:[(25\:\times\:4)\:-8\:-\:2]}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:900\:\div\:[(100)\:-\:8\:-\:2]}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:900\:\div\:[(100)\:-\:10]}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:900\:\div\:90}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:10}$

示例 8 - 简化以下方程式 $\mathrm{(25\:\times\:4)\:-\:(20\:\times\:4)}$

解 - 给定方程式为 $\mathrm{(25\:\times\:4)\:-\:(20\:\times\:4)}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:100\:-\:8}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:20}$

示例 9 - 如果一个单元测试包含 100 道题，每答对一题得 10 分，每答错一题扣 4 分。如果维诺德正确回答了 75 道题，并且他尝试了所有问题。维诺德的总分是多少？

解 - 单元测试中的问题总数 = 100

每道正确问题的得分 = 10

每道错误问题扣除的分数 = 4

他尝试的问题总数 = 100

维诺德的总分 $\mathrm{=\:75\:\times\:10\:-\:(25\:\times\:4)}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:750\:-\:100}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:650}$

示例 10 - 如果一辆公共汽车以 $\mathrm{10\:\frac{m}{s}}$ 的速度行驶 10 分钟，则求公共汽车行驶的总距离。

解 $\mathrm{10\:\frac{m}{s}}$

$\mathrm{总时间\:=\:10\:分钟}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:10\:\times\:60\:=\:600\:秒}$

$\mathrm{公共汽车行驶的距离\:=\:600\:\times\:10}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:600\:米}$

结论

整数练习题涵盖了整数的加法和减法、多个整数的加法和减法以及不同整数的乘法和除法。整数可以包含正整数和负整数，包括零，是一个没有小数或分数部分的数字。

常见问题解答

1. 整数是什么意思？

整数可以包含正整数和负整数，包括零，是一个没有小数或分数部分的数字

2. 负整数可能吗？

是的，负整数是可能的。负整数，例如 -1、-2、-3、-4 等，是自然数的加法逆元。

3. 数学中有多少种整数？

整数有三种类型：正整数、零和负整数

4. 正整数是什么意思？

如果一个数大于零，则它被认为是正数。例如，1、2、3 等。

5. 负整数是什么意思？

负数是小于零的数。例如 - -1、-2、-3 等

6. 如何在数轴上画整数？

在数轴上绘制整数需要遵循以下步骤。

• 正整数位于数字零的右侧，因为它们大于 0。

• 负数位于零的左侧，因为它们小于 0。

• 零通常位于中间，因为它既不能是正数也不能是负数。