数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究峰度 – 定义、示例、类型
峰度是一个统计术语，用于量化类似于偏度的分布。与仅区分一个尾部中的绝对值与另一个尾部中的绝对值的偏度不同，峰度评估两个尾部的极值。在具有强峰度的分布中，尾部数据超过正态分布的尾部。低峰度的范围的尾部通常不如正态循环的尾部严重。
高峰度是投资者密切关注的一种趋势，因为它可能导致利润或损失的两个方向都会出现更尖锐的结果。这与正常偏差或常规变化相比。峰度风险是赋予此指标的名称，该指标向投资者发出了有关其资产的信号。
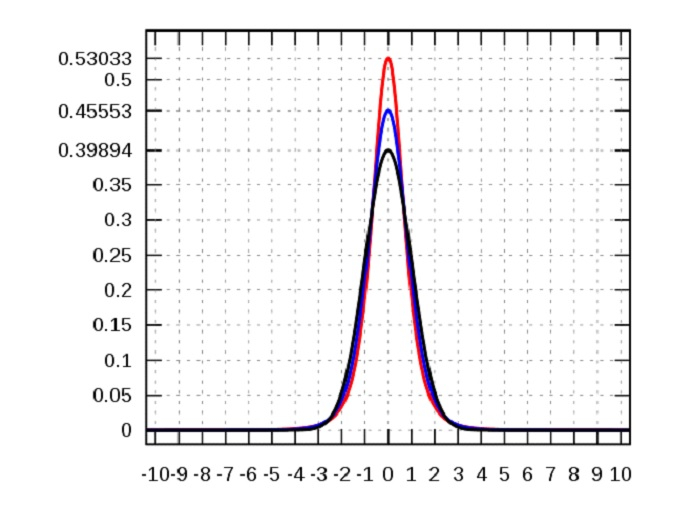
什么是峰度？
峰度衡量分配尾部相对于分布中心的总权重。当使用直方图绘制正态数据时，可以观察到一个钟形峰值，其中大部分数据位于均值的 +/- 变化范围内三个标准偏差内。在强峰度期间，此钟形直方图倾向于超出正常变化的长度。
在此统计工具中，有时在分布峰值发生时会出现混淆。必须记住，峰度是形状图，与完整形状相比，它提供了关于分布尾部的整体情况。
在低峰度的情况下，分布也可以非常尖锐，而在无限峰度的情况下，它可以完全正常或平坦，没有任何偏差。因此，此工具计算并更多地关注“尾端性”，而不是峰值。
峰度的不同类型有哪些？
给定分布的超额峰度决定了峰度的形式。超额峰度可以是正的或负的，也可以接近于零。
正态分布 - 超额峰度
这种类型的模式通常以其超额峰度为零或接近零而被识别，这在遵循正态分布的数据中可见。如果数据遵循正态分布，则表明数据具有正态分布。
尖顶分布 – 正超额峰度
尖顶分布表示正偏峰度。它的特征是在两侧都有巨大的尾部，并且存在大量异常值。对于投资者而言，这可能意味着结果将是正或负的极端。因此，此图表可能表明投资者在分布的两侧进行投资的风险模式。
扁平分布 – 负超额峰度
扁平分布中的超额峰度为负，其特征是扁平尾部分布。扁平尾部表示分布中的较小异常值。在金融环境中，投资回报的扁平分布对投资者有利，因为这意味着更高的投资回报。
2K+ 次查看
