数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究数据结构中的层级链接(2,4)树
在本节中，我们将解释如何通过引入层级链接，(2,4)树能够支持高效的指搜索。本节中解释的思想也适用于更一般的平衡高度树类，表示为(a, b)树，其中b ≥ 2a。
(2,4)树定义为一种平衡高度搜索树，其中所有叶子节点具有相同的深度，并且所有内部节点的度数为二、三或四。元素存储在叶子节点中，内部节点仅存储搜索键以指导搜索。由于每个内部节点的度数至少为二，因此(2,4)树的高度为O(log n)，并且支持在O(log n)时间内进行搜索。 (2,4)树的一个重要特性是，由手指提供的插入和删除操作的摊销时间为O(1)（此属性不适用于(2, 3)树，在(2, 3)树中，存在m次插入和删除操作的序列需要Θ(m log m)时间）。此外，具有m个叶子节点的(2,4)树可以拆分为大小为m1和m2的两棵树，摊销时间为O(log min(m1, m2))。类似地，大小为m1和m2的两棵(2,4)树可以在摊销时间O(log min(m1, m2))内连接（串联）。
为了支持指搜索，(2,4)树通过层级链接进行增强，使得所有具有相同深度的节点都通过双向链表链接在一起。下图显示了一个带有层级链接的(2,4)树。请记住，所有边都表示双向链接。在(2,4)树的插入、删除、拆分和连接过程中，额外的层级链接很容易维护。
为了完成从X到Y的指搜索，我们首先检查Y是否在X的左侧或右侧。假设Y在X的右侧（不失一般性）。然后，我们访问从X到根节点的路径，同时检查路径上的节点V及其右侧邻居，直到确定Y包含在以V或V的右侧邻居为根的子树中。然后终止向上搜索，并在V和/或V的右侧邻居处分别启动最多两个向下搜索y。在图1中，从j到t的指搜索过程中跟随的指针用粗线表示。
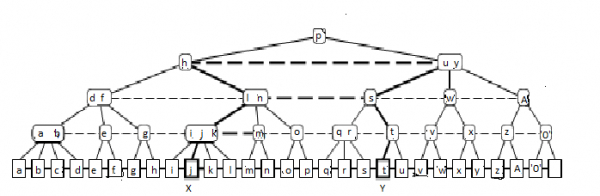
O(log d)搜索时间来自以下观察：如果我们将向上搜索推进到节点V的父节点，则Y位于V的右侧邻居的最左侧子树的右侧，即d至少以迄今为止达到的高度呈指数增长。
在图1中，我们从标记为“l n”的内部节点推进到标记为“h”的节点，因为从“s”我们知道Y位于以节点“q r”为根的子树的右侧。
层级链接(2,4)树的构造可以直接推广到层级链接(a, b)树，该树可以在外部存储器中实现。通过选择a = 2b和b，使得内部节点适合外部存储器中的一个块，我们实现了支持在O(1)内存传输中进行插入和删除以及在O(logb n)内存传输中进行指搜索的外部存储器指搜索树。
515 次浏览
