数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学每两层改变方向的层序遍历（C/C++ 实现）
层序遍历
这是一种通过深度优先遍历处理或打印二叉树所有节点的算法，从根节点开始，依次遍历其子节点，以此类推。
示例
输入 −
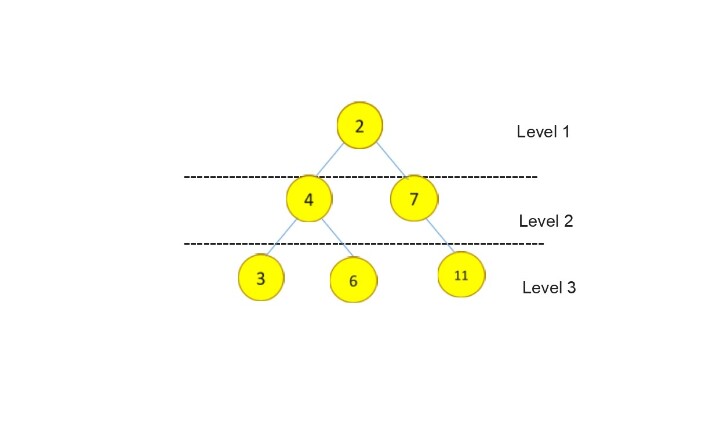
输出 −
2 4 7 3 6 11
此任务涉及打印二叉树的层序遍历，前两层从右到左打印，接下来的两层从左到右打印，依次类推。挑战在于二叉树的层序遍历必须每两层反转一次。
请参考示例输入以更好地理解问题。
输入 −
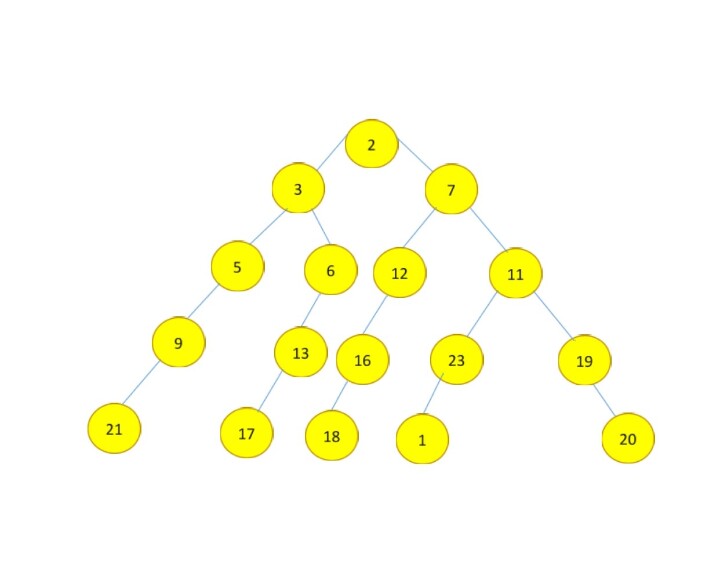
输出 −
2 3 7 11 12 6 5 19 23 16 13 9 21 17 18 1 20
在上图中，第 1 层和第 2 层从左到右打印，然后是第 3 层和第 4 层，它们从右到左打印，第 5 层从左到右打印。
方法
我们将使用队列和栈来解决这个问题。每两层之后，使用栈来改变遍历方向，队列用于正常的层序遍历。
使用标准的层序遍历方法打印二叉树的前两层。
我们将声明两个变量：`count=0` 用于存储我们正在遍历的层级，以及一个名为 `rightToLeft=false` 的布尔变量，用于从右到左打印元素。
每当 `count=2` 时，我们将 `!rightToLeft` (非运算) 存储到 `rightToLeft` 中，并将 `count` 设置为 0。
当 `rightToLeft=true` 时，我们将节点压入栈中，而不是打印它们。一旦当前层的节点都压入栈中，我们就打印栈中的节点。
因为栈遵循后进先出 (LIFO) 的原则，所以我们可以使用栈来反向打印节点。
接下来的两层，我们将使用层序遍历方法从左到右打印节点，然后再次使用栈从右到左打印接下来的两层节点，以此类推。
通过结合使用队列和栈，我们可以实现每两层改变方向的层序遍历。
示例
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
class TreeNode{
public:
int data;
TreeNode*left;
TreeNode*right;
TreeNode (int d){
data=d;
left=NULL;
right=NULL;
}
};
void printEveryTwoLevelOrderTraversal(TreeNode* root){
//when the node is null
if(root==NULL){
return;
}
// when root left and right is null
if(root->left==NULL && root->right==NULL){
cout<<root->data<<endl;
return;
}
queue<TreeNode*> Queue; // queue is for traversing the level
stack<TreeNode*> Stack; // stack is for printing the node in reverse order once popped out from the queue
int count=0;
bool direction = false;
Queue.push(root); // root node is pushed inside the queue
while(!Queue.empty()){
int size=Queue.size();
count++;
for(int i=0;i<size;i++){
TreeNode* tmp=Queue.front();
Queue.pop();
if(direction==false){ // print the node from left to right once the node is popped out from the queue
cout<<tmp->data<<" ";
}
else{ // it stores the node in the stack for printing right to left
Stack.push(tmp);
}
if(tmp->left!=NULL){
Queue.push(tmp->left);
}
if(tmp->right!=NULL){
Queue.push(tmp->right);
}
}
if(direction==true){
while(!Stack.empty()){
TreeNode* tmp=Stack.top();
Stack.pop();
cout<<tmp->data<<" ";
}
}
if(count==2){ // change the direction after every two level
direction=!direction;
count=0;
}
cout<<endl;
}
}
int main(){
TreeNode* node=new TreeNode(5);
node->left=new TreeNode(7);
node->right=new TreeNode(8);
node->left->left=new TreeNode(4);
node->left->right=new TreeNode(9);
node->left->left->left=new TreeNode(10);
node->left->left->right=new TreeNode(14);
node->right->left=new TreeNode(11);
node->right->right=new TreeNode(12);
printEveryTwoLevelOrderTraversal(node);
return 0;
}
输出
5 7 8 12 11 9 4 14 10
时间复杂度：O(n)。 时间复杂度为 O(n)，因为每个节点在遍历过程中最多只遍历两次。
空间复杂度：O(n)，因为二叉树中节点的数量将是栈或队列的大小。
在本文中，我们尝试解释如何打印每两层改变方向的层序遍历。我希望这篇文章能帮助你理解这个概念。
123 次浏览
