数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物
数学
英语
经济学
心理学
社会学
时尚研究
法律研究用 C++ 编程逐行打印层级遍历。
给定二叉树，函数必须逐行找出树的层级遍历。
层级遍历：左中右，这意味着首先打印节点的左子树，然后打印根的值，然后转到右子树，但在这里我们必须逐行进行，从左开始，在给定二叉树的右节点结束。
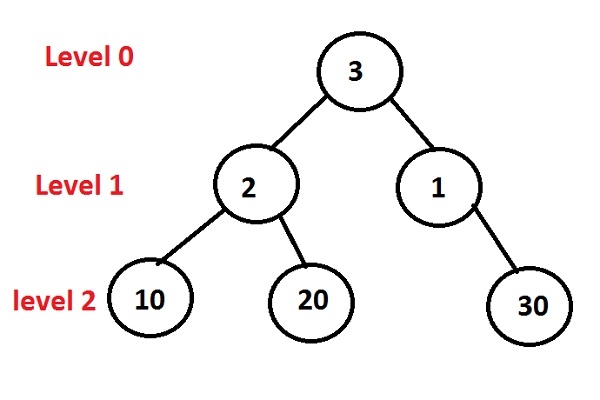
上面给出的二叉树将生成以下输出 −
Level 0: 3 Level 1: 2 1 Level 2: 10 20 30
算法
START Step 1 -> create a structure of a node as struct node struct node *left, *right int data End Step 2 -> function to create a node node* newnode(int data) node *temp = new node temp->data = data temp->left = temp->right= NULL return temp step 3 -> function for inorder traversal void levelorder(node *root) IF root = NULL Return End queue<node *> que que.push(root) Loop While que.empty() = false int count = que.size() Loop While count > 0 node *node = que.front() print node->data que.pop() IF node->left != NULL que.push(node->left) End IF node->right != NULL que.push(node->right) End Decrement count by 1 End End Step 4 -> In main() function Create tree using node *root = newnode(3) Call levelorder(root) STOP
示例
#include <iostream>
#include <queue>
using namespace std;
//it will create a node structure
struct node{
struct node *left;
int data;
struct node *right;
};
void levelorder(node *root){
if (root == NULL)
return;
queue<node *> que;
que.push(root);
while (que.empty() == false){
int count = que.size();
while (count > 0){
node *node = que.front();
cout << node->data << " ";
que.pop();
if (node->left != NULL)
que.push(node->left);
if (node->right != NULL)
que.push(node->right);
count--;
}
}
}
//it will create a new node
node* newnode(int data){
node *temp = new node;
temp->data = data;
temp->left = NULL;
temp->right = NULL;
return temp;
}
int main(){
// it will generate the binary tree
node *root = newnode(3);
root->left = newnode(2);
root->right = newnode(1);
root->left->left = newnode(10);
root->left->right = newnode(20);
root->right->right = newnode(30);
levelorder(root);
return 0;
}输出
如果我们运行上述程序，它将生成以下输出
3 2 1 10 20 30
更新于： 04-Sep-2019
316 次浏览
广告