数据结构
网络
关系型数据库管理系统 (RDBMS)
操作系统
Java
Microsoft Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
JavaScript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学机器学习中的最大似然估计
简介
最大似然法是一种常用的密度估计方法，它定义了一个似然函数来获取分布数据的概率。学习和理解最大似然法的概念至关重要，因为它是学习其他高级机器学习和深度学习技术和算法的必要核心概念之一。
在本文中，我们将讨论似然函数、其背后的核心思想以及它如何结合代码示例工作。这将有助于更好地理解这个概念并在需要时应用它。
让我们先深入了解似然函数，以便理解最大似然估计。
什么是似然？
在机器学习中，似然是衡量数据观测值的一种指标，它可以告诉我们对于特定数据点，结果或目标变量的值。简单来说，顾名思义，似然函数告诉我们特定数据点与现有数据分布的匹配程度。
例如，假设数据集中有两个数据点。如果第一个数据点的似然值大于第二个数据点，那么可以假设第一个数据点为最终模型提供了更准确的信息，因此对于模型来说更有价值和精确。
在讨论之后，你可能会产生一个疑问：如果似然函数的工作方式与概率函数相同，那么它们有什么区别呢？
概率和似然的区别
虽然概率和似然的工作原理和直觉看起来相同，但存在细微的差别：似然是一个函数，它定义或告诉我们特定数据点在数据分布中有多大的价值以及对最终算法的贡献程度，以及它对机器学习算法的适用性。
而概率，简单来说，是一个描述某事件或事物发生的几率的术语，通常是相对于其他情况或条件而言的，大多被称为条件概率。
此外，与特定问题相关的所有概率之和为1，且不能超过1，而似然值可以大于1。
什么是最大似然估计？
在讨论了似然函数的直觉之后，我们清楚地知道，每个模型都需要更高的似然值才能获得准确的模型和准确的结果。因此，这里“最大似然”这个术语表示我们正在最大化似然函数，称为**似然函数的最大化**。
让我们尝试用一个例子来理解。
假设我们有一个分类数据集，其中自变量是学生在特定考试中取得的分数，而目标变量或因变量是分类变量，具有“是”和“否”属性，表示学生是否在校园招聘中被录用。
现在，如果我们尝试使用最大似然估计来解决这个问题，该函数将首先根据目标变量的每个适用条件计算每个数据点的概率。在下一步中，该函数将在二维图中绘制所有数据点，并尝试找到最适合数据集的线，将其分成两部分。最佳拟合线将在一些迭代后获得，一旦获得，该线将通过简单地将其绘制到图中来对数据点进行分类。
最大似然：基础
最大似然估计是用于解决分类问题的某些机器学习和深度学习方法的基础。一个例子是逻辑回归，其中该算法用于使用图上最佳拟合线对数据点进行分类。关于深度学习算法，同样的方法被称为感知器技巧。
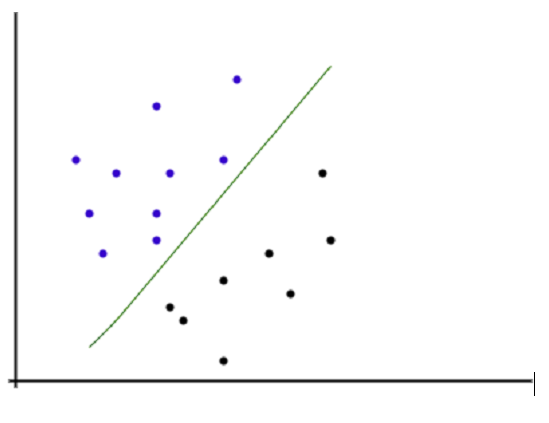
如上图所示，所有数据观测值都绘制在二维图中，其中X轴表示自变量或训练数据，Y轴表示目标变量。绘制一条线来分离正负数据观测值。根据算法，落在线以上的数据点被视为正数据点，落在线以下的数据点被视为负数据点。
最大似然估计：代码示例
我们可以使用逻辑回归快速实现任何分类数据集的最大似然估计技术。让我们尝试实现它。
import pandas as pd import numpy as np import seaborn as sns from sklearn.linear_model import LogisticRegression lr=LogisticRegression() lr.fit(X_train,y_train) lr_pred=lr.predict(X_test) sns.regplot(x="X",y='lr_pred',data=df_pred ,logistic=True, ci=None)
以上代码将针对给定的数据集拟合逻辑回归，并生成数据的线图，表示数据的分布以及根据算法获得的最佳拟合。
关键要点
最大似然是一个函数，它描述了数据点及其与模型的最佳拟合程度。
最大似然与概率方法不同，概率方法基于计算概率的原理。相反，似然方法试图根据数据分布最大化数据观测值的似然。
最大似然法是一种用于解决密度分布问题的算法，是某些算法（如逻辑回归）的基础。
这种方法非常相似，在深度学习方法中主要被称为感知器技巧。
结论
在本文中，我们讨论了似然函数、最大似然估计、其核心直觉和工作机制，以及一些关键要点相关的实际示例。这将帮助人们更好地更深入地理解最大似然，并有效地回答相关面试问题。
14K+ 次浏览
