机器学习中的稳健相关性

---

在本教程中，我们将学习机器学习中的稳健相关性。了解和评估不同的相关性在各种业务中都很有用。

什么是相关性？

两个实体之间的统计关系称为相关性。或者说，它描述了两个变量的运动之间的关系。相关性也可以使用不同的数据集。在某些情况下，您可能已经猜到某些事件将如何相互关联，但在其他情况下，相关性可能会让您感到意外。重要的是要认识到相关性并不意味着因果关系。散点图是数据拟合的一个例子。一般来说，可以使用散点图来评估变量之间是否存在相关性。

不同类型的相关性

正相关

如果关系中的两个变量都朝相同的方向移动，则该关系被称为正相关。因此，当一个变量随着另一个变量的增加而增加，或者当一个变量随着另一个变量的减少而减少时。身高和体重是两个显示正相关关系的变量。

负相关

负相关是两个变量之间的关系，其中一个变量的增加会导致另一个变量的减少。海拔高度和温度是负相关的两个例子。当你爬山（高度增加）时，气温会下降（温度下降）。

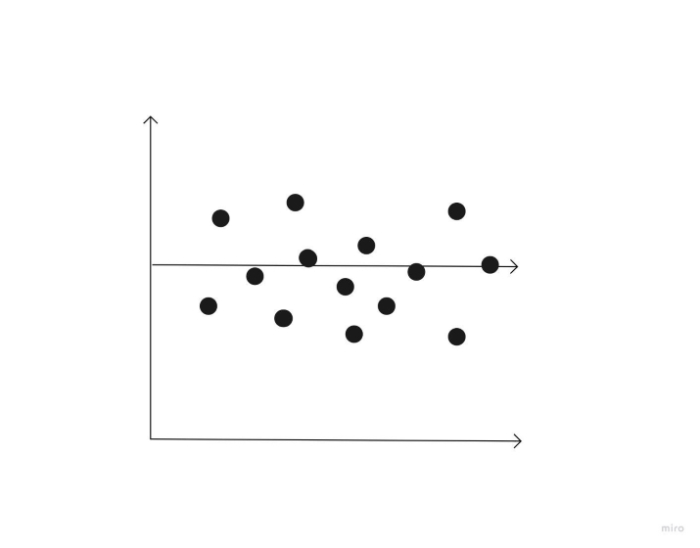
零相关

0 的相关性表示两个变量之间没有关系。换句话说，当一个变量朝一个方向移动时，另一个变量朝完全不同的方向移动。

什么是相关系数？

相关系数是指一个变量的值的变化在多大程度上可以预测另一个变量的值的变化的统计量度。当可以通过另一个变量的变化准确预测一个变量的变化时，人们倾向于假设一个变量的变化一定是另一个变量变化的结果。然而，相关性并不能证明因果关系。这两个变量都可能受到某个未知因素的类似影响。在消费者数据模式方面，了解相关性和因果关系之间的区别可能很有用，并提供有见地的信息。

相关系数评估两个变量之间的相关程度，而相关性分析两个事物如何相互关联。统计学中存在三种不同的相关系数。

其中一些是：

• 皮尔逊相关性 - 皮尔逊相关性是最常用的确定两个变量之间是否存在线性关系的方法。根据这两个数据集的相关性强弱，它将更接近 +1 或 -1。例如，在确定两只证券之间如何相互关联时，皮尔逊 r 相关性用于评估两只证券之间股票市场相关性的程度。

• 斯皮尔曼相关性 - 此类相关性用于确定两个数据集之间的单调关系或联系。与皮尔逊相关系数不同，它使用偏斜或有序变量而不是正态分布变量，并且基于每个数据集的排名值。当变量至少以有序尺度进行评估时，它是合适的相关性分析。此系数需要一个数据表，其中包含原始数据、其排名以及两个排名之间的差异。

• 肯德尔相关性 - 此类相关性评估两个数据集之间相互依赖的程度。肯德尔等级相关性是一种非参数检验，用于评估两个变量之间的依赖程度。

您将使用哪种形式的相关系数取决于您对变量的了解。使用适当的相关方程将提高您理解正在检查的数据集之间关系的能力。

公式相关性

要确定相关性，请使用以下公式：

$$\mathrm{\frac{(x(i) − x)(y(i) − \bar{y})}{\sum(x(i) − \bar(x))^2 \: \sum(y(i) − (\bar{y}))^2}}$$

考虑以下表示形式以确定相关性：

• x(i) = x 的值
• y(i) = y 的值
• x̅= x 值的平均值
• ȳ= y 值的平均值

如何计算相关性？

可以使用多种技术来计算相关性。此页面详细介绍了最常用的技术，即皮尔逊积矩相关性。皮尔逊积矩相关性分析一对变量的线性关系。任何具有有限协方差矩阵的数据集都适合使用它。

以下是计算相关性的步骤。

• 收集 x 变量和 y 变量的信息。

• 应确定 x 均值变量以及 y 均值变量。

• 从 x 变量的每个值中减去 x 变量的平均值。对 y 变量重复此过程。

• 将 x 变量的平均值与值之间的每个差异除以 y 变量中相应的差异。

• 通过对这些差异中的每一个求平方来添加答案。

• 计算步骤 5 中值的平方根。

• 将步骤 4 的结果除以步骤 6 的结果。

结论

通过观察和比较消费者对各种营销策略的反应，营销专家利用相关性分析来评估广告系列的有效性。他们能够更好地理解并以这种方式帮助他们的客户。

对于根本原因分析，相关性分析非常有用，并且减少了数据科学家和负责监控数据的人员的发现时间 (TTD) 和修复时间 (TTR)。通过同时或以相同的速度观察两个意外事件或异常情况，可以更容易地找到问题的原因。如果能够尽早识别和解决问题，则组织的成本将降低。

相关性通常用于心理学研究，但是，重要的是要认识到相关性并不意味着因果关系。如果您喜欢处理数据，它是您最好的朋友。它假设一个可能不存在的因果关系，并且是那些不熟悉统计学的人常犯的一个错误。