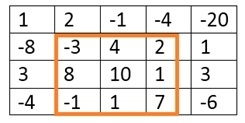
二维矩阵中的最大和矩形
已给出一块矩阵。我们需要找出和最大的矩形(有时是正方形)矩阵。
这种算法背后的思想是固定左右两列并尝试找出从左列到右列的各个行的元素和,并将其暂时存储起来。我们将尝试找出顶部和底部行号。在获得临时数组后,我们可以应用 Kadane 算法来获得最大和子数组。有了它,整个矩形将形成。
输入和输出
Input: The matrix of integers. 1 2 -1 -4 -20 -8 -3 4 2 1 3 8 10 1 3 -4 -1 1 7 -6 Output: The top left point and bottom right point of the submatrix, and the total sum of the submatrix. (Top, Left) (1, 1) (Bottom, Right) (3, 3) The max sum is: 29
算法
kadaneAlgorithm(array, start, end, n)
输入:数组将保存和、开始和结束点、元素数。
输出 − 找出开始和结束点。
Begin sum := 0 and maxSum := - ∞ end := -1 tempStart := 0 for each element i in the array, do sum := sum + array[i] if sum < 0, then sum := 0 tempStart := i + 1 else if sum > maxSum, then maxSum := sum start := tempStart end := i done if end ≠ -1, then return maxSum maxSum := array[0], start := 0 and end := 0 for each element i from 1 to n of array, do if array[i] > maxSum, then maxSum := array[i] start := i and end := i done return maxSum End
maxSumRect(矩阵)
输入:给定的矩阵。
输出:矩形的最大和。
Begin maxSum := - ∞ define temp array, whose size is same as row of matrix for left := 0 to number of columns in the Matrix, do till temp array with 0s for right := left to column of matrix -1, do for each row i, do temp[i] := matrix[i, right] done sum := kadaneAlgorithm(temp, start, end, number of rows) if sum > maxSum, then maxSum := sum endLeft := left endRight := right endTop := start endBottom := end done done display top left and bottom right corner and the maxSum End
示例
#include<iostream>
#define ROW 4
#define COL 5
using namespace std;
int M[ROW][COL] = {
{1, 2, -1, -4, -20},
{-8, -3, 4, 2, 1},
{3, 8, 10, 1, 3},
{-4, -1, 1, 7, -6}
};
int kadaneAlgo(int arr[], int &start, int &end, int n) { //find max sum and starting and ending location
int sum = 0, maxSum = INT_MIN;
end = -1; //at first no place is selected
int tempStart = 0; //starting from 0
for (int i = 0; i < n; i++) {
sum += arr[i];
if (sum < 0) {
sum = 0;
tempStart = i+1;
}else if (sum > maxSum) { //get maximum sum, and update start and end index
maxSum = sum;
start = tempStart;
end = i;
}
}
if (end != -1)
return maxSum;
//when all elements are negative in the array
maxSum = arr[0];
start = end = 0;
// Find the maximum element in array
for (int i = 1; i < n; i++) {
if (arr[i] > maxSum) {
maxSum = arr[i];
start = end = i;
}
}
return maxSum;
}
void maxSumRect() {
int maxSum = INT_MIN, endLeft, endRight, endTop, endBottom;
int left, right;
int temp[ROW], sum, start, end;
for (left = 0; left < COL; left++) {
for(int i = 0; i<ROW; i++)//temp initially holds all 0
temp[i] = 0;
for (right = left; right < COL; ++right) {
for (int i = 0; i < ROW; ++i) //for each row, find the sum
temp[i] += M[i][right];
sum = kadaneAlgo(temp, start, end, ROW); //find sum of rectangle (top, left) and (bottom right)
if (sum > maxSum) { //find maximum value of sum, then update corner points
maxSum = sum;
endLeft = left;
endRight = right;
endTop = start;
endBottom = end;
}
}
}
cout << "(Top, Left) ("<<endTop<<", "<<endLeft<<")"<<endl;
cout << "(Bottom, Right) ("<<endBottom<<", "<<endRight<<")"<<endl;
cout << "The max sum is: "<< maxSum;
}
int main() {
maxSumRect();
}输出
(Top, Left) (1, 1) (Bottom, Right) (3, 3) The max sum is: 29

广告

 数据结构
数据结构 网络
网络 关系型数据库管理系统
关系型数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 编程
C 编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP