线段的绘制方法

---

简介

• 顾名思义，线段是具有两个端点的一条线的某一部分。

• 它是实用几何的基本组成部分之一，使构建几何图形和形状变得更加容易。

• 连接两点的直线的一部分称为线段。

• 具有端点 A 和 B 的线段的符号为 AB。

• 但是，您如何绘制线段？我们用来测量线段的工具是否与我们用来绘制它的工具相同？在本教程中，我们将探讨绘制线段的方法。

线段

• 在几何学中，线段在其上具有两个不同的点，定义了其边界。

• 线段有时被称为连接两点的线的一部分。

• 线和线段的区别在于，线没有端点，并且可以无限延伸到任一方向。

• 射线只有一个端点和一个无限长的另一端，而线段则有两个端点。

在下图中，AB 是直线 l 上的一部分线段

如何绘制线段

具有起点和终点的线的一部分称为线段。线段符号，顶部的横线，表示其特定长度。可以使用以下任何方法创建特定长度的线段：

• 使用尺子绘制线段

• 使用尺子和圆规绘制线段

使用尺子

最简单和最直接的方法是使用尺子创建适当长度的线段。我们按照以下步骤使用尺子绘制线段：

步骤1 - 首先取一把尺子，找到其零点起点。

步骤2 - 将尺子放在纸上，并在每个线段的开头标记一个点，将其标记为 P。

步骤3 - 标记线段的终点，直到所需的长度，例如 10 厘米，将其标记为 Q。

步骤4 - 通过绘制一条直线连接这两个点。我们将得到一条长 10 厘米的线段 PQ。

使用圆规和尺子

圆规和尺子也可以用来绘制线段。虽然它需要更多的注意力，但这种方法可能被认为更准确。我们按照以下步骤使用尺子和圆规绘制线段：

步骤1 - 绘制任意长度的直线，标记点 P。

步骤2 - 线段的起点。使用尺子将圆规的指针对齐到 P，并将其打开，以便铅笔的笔尖位于 Q 处，Q 距离 P 4.5 厘米。

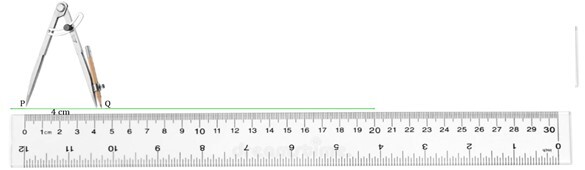
已知三边构造三角形

提供的信息将决定三角形的构造方式。在这里，我们将了解当我们知道其三条边的长度时如何构造三角形。在开始构造三角形之前，必须满足以下关键三角形属性，才能满足所有三条边的长度。该属性指出，任何两个三角形边的和始终大于三角形的第三边。如果给定的三边不满足上述三角形的属性，我们将无法构造三角形。当已知所有三条边的长度时，尺子和圆规，即数学工具是构造三角形所必需的。

例如

假设 PQ 为 4 厘米，QR 为 6 厘米，PR 为 5 厘米，构造三角形 PQR。

构造

步骤 1 - 绘制线段 QR=6cm。（这里我们取最长的边）

步骤 2 - 以“Q”为圆心，在直线 QR 上方绘制半径为 4 厘米的弧。

步骤 3 - 以“R”为圆心，绘制半径为 5 厘米的弧，与先前的弧相交于“P”

步骤 4 - 连接 PQ 和 PR。现在 PQR 是所需的三角形。

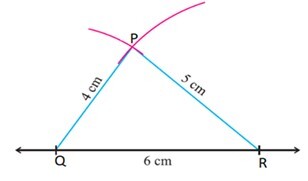
当使用圆规和直尺或尺子指定所有三条边的长度时，此结构演示了如何轻松地构造三角形。

解题示例

1. 使用尺子绘制一条长度为 8.5 厘米的线段 LM。

解答

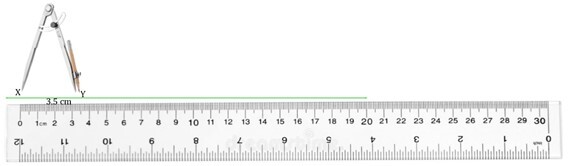
2. 使用尺子和圆规构造一条长度为 3.5 厘米的线段 XY。

解答

步骤一中创建任意长度的直线。标记点 X，即线段的起点。使用尺子将圆规的指针对齐到 X，并将其打开，以便铅笔的笔尖位于 Y 处，Y 距离 X 3.5 厘米，如下所示：

3. 已知三边构造三角形的步骤是什么？

解答

以下是绘制三角形 XYZ 的步骤，已知 XY 为 8 厘米，YZ 为 12 厘米，XZ 为 10 厘米。

步骤 1 - 绘制线段 YZ=12 cm。（这里我们取最长的边）

步骤 2 - 以“Y”为圆心，在直线 YZ 上方绘制半径为 8 厘米的弧。

步骤 3 - 以“Z”为圆心，绘制半径为 10 厘米的弧，与先前的弧相交于“X”

步骤 4 - 连接 XY 和 XZ。现在 XYZ 是所需的三角形。

结论

正如本教程中所讨论的，我们可以使用尺子和圆规和尺子来绘制线段。但在绘制时，我们必须记住以下几点，以防止出现错误，在绘制线段时，要直接向下看尺子。不要忘记确保圆规的顶部铰链固定好，以防止滑动。牢牢抓住铅笔的握把，以防止滑动，但不要捏得太紧，否则圆的直径会改变。确保铅笔笔芯与圆规的针头对齐。

常见问题解答

1. 我们为什么要使用线段？

由于线段有起点和终点，因此可以测量线段。由于线段具有固定的长度，因此可以用来表示任何多边形的边。射线不能测量，因为它只有一个起点，没有终点。

2. 如何测量线段？

线段使用尺子测量。在尺子的两条边上，标记了英寸和厘米。

3. 线段有多少种不同类型？

线段有四种不同的类型。

4. 线段可以弯曲吗？

通过连接平面上的两点可以创建一条直线段。但是，当连接曲面上的两点时，会创建一条曲线段。

5. 线段的长度是多少？

可以使用线段两个端点之间的距离来计算其长度。它是连接这两点的路径，并且具有已知的长度。