(a) 根据下图所示的电阻组合，求M点和N点之间的等效电阻。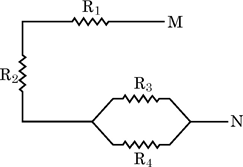(b) 说明焦耳定律。(c) 为什么一个消耗功率为1 kW，电压为220 V的电熨斗需要一个5 A的保险丝？(d) 为什么将一个电灯泡和一个电加热器串联起来是不切实际的？

(a) 已知

 电阻阻值 = $R_1, R_2, R_3,\ 和\ R_4$

求解：M点和N点之间的等效电阻，$(R_eq)$。

解答

从图中可以看出，$R_3$和$R_4$是并联的。

我们知道，当两个导体的电阻并联时，总电阻为：

$\frac {1}{R_p}=\frac {1}{R_3}+\frac {1}{R_4}$

$\frac {1}{R_p}=\frac {R_4+R_3}{R_3\times {R_4}}$

${R_p}=\frac {R_3\times {R_4}}{R_4+R_3}$

现在，$R_1$，$R_2$和$R_p$是串联的。

则等效电阻为：

$R_eq=R_1+R_2+R_p$

$R_eq=R_1+R_2+\frac {R_3\times {R_4}}{R_4+R_3}$

因此，M点和N点之间的等效电阻$(R_eq)$为$R_1+R_2+\frac {R_3\times {R_4}}{R_4+R_3}$。

(b) 焦耳定律指的是，由导体产生的热量与导体的电阻(R)和通过导体的电流的平方成正比，还与通电时间成正比。

焦耳定律的数学表达式是

$H=I^2Rt$

其中，

$H$ = 热效应。

$I$ = 流过导体的电流。

$R$ = 导体的电阻。

$t$ = 时间。

(c) 已知

电压，$V$ = 220 V

功率，$P$ = 1 kW = 1000 W

保险丝电流，$I$ = 5 A

求解：电路中的电流，$I$。

解答

我们知道，功率为：

$P=V\times {I}$

代入已知值，我们得到：

$1000=220\times {I}$

$I=\frac{1000}{220}$

$I=4.54A$

因此，电路中的电流为4.54A。

我们应该使用电流容量略大于设备（此处为电熨斗）最大电流的保险丝。因此，需要一个5 A的保险丝，因为它略大于4.54 A。现在，如果电流值超过5 A，保险丝就会熔断。

(d) 将电灯泡和电加热器串联起来是不切实际的，因为它们将无法获得满足其需求的电流和电压。