计算下列各图中 $x$ 的值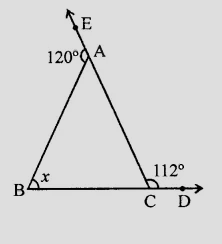："\n

已知

在 $\triangle ABC$ 中，边 $BC$ 和 $CA$ 分别延长到 $D$ 和 $E$。

$\angle \mathrm{ACD}=112^{\circ}$ 且 $\angle \mathrm{BAE}=120^{\circ}$

要求

我们需要计算 $x$ 的值。

解答

$\angle \mathrm{ACB}+\angle \mathrm{ACD}=180^{\circ}$

$\angle \mathrm{ACB}+112^{\circ}=180^{\circ}$

$\angle \mathrm{ACB}=180^{\circ}-112^{\circ}=68^{\circ}$

类似地，

$\angle \mathrm{BAE}+\angle \mathrm{BAC}=180^{\circ}$

$120^{\circ}+\angle \mathrm{BAC}=180^{\circ}$

$\angle \mathrm{BAC}=180^{\circ}-120^{\circ}=60^{\circ}$

$\angle \mathrm{BAC}+\angle \mathrm{ABC}+\angle \mathrm{BCA}=180^{\circ}$

$60^{\circ}+x+68^{\circ}=180^{\circ}$

$128^{\circ}+x=180^{\circ}$

$x=180^{\circ}-128^{\circ}=52^{\circ}$

因此，$x$ 的值为 $52^{\circ}$。

教程点

更新于： 2022年10月10日

46 次浏览

开启你的 职业生涯

完成课程，获得认证

开始学习