在已知射线的起点作一个90°角，并说明作图的理由。

待办事项

我们需要在已知射线的起点作一个90°角，并说明作图的理由。

解答

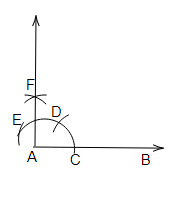
作图步骤

(a) 画一条射线AB。

(b) 以A为圆心，适当的半径画弧，使它与AB相交于C。

(c) 以C为圆心，相同的半径在上面画弧与D相交。

(d) 以D为圆心，相同的半径在上面画弧与E相交。

(e) 以D和E为圆心，半径大于$\frac{1}{2}DE$画两条弧，在F点相交。

(f) 连接AF并延长形成射线AF。

因此，

$\angle BAF = 90^o$。

证明

证明$\angle BAF=90^o$

让我们从A到D和O到E画一条虚线。

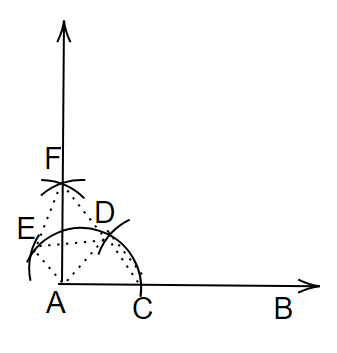
我们有，

$AC=CD=AD$

因此，

$ACD$是一个等边三角形

这意味着，

$\angle CAD=60^o$

同样地，我们得到，

$AE=DE=AD$

因此，

$ADE$是一个等边三角形

这意味着，

$\angle EAD=60^o$

根据SSS全等定理，我们得到，

$\triangle ACD \cong \triangle ADE$

根据全等三角形对应角相等，我们得到，

$\angle CAD=\angle EAD$

因此，

$\angle DAF=\frac{1}{2}\angle EAD=\frac{1}{2}(60^o)=30^o$

这意味着，

$\angle DAF=30^o$

$\angle BAF=\angle BAD+\angle DAF$

$=60^o+30^o$

$=90^o$

因此，证明完毕。

教程点

更新于：2022年10月10日

56 次浏览

启动你的职业生涯

完成课程获得认证

开始学习