已知等边三角形的边长，作图构造该等边三角形并说明作图依据。

待办事项

我们需要构造一个等边三角形，已知其边长，并说明构造的依据。

解答

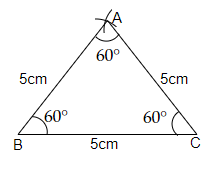
作图步骤

(i) 作一条线段 $BC$，长度为 $5\ cm$。

(ii) 以点 $B$ 为圆心，半径为 $5\ cm$ 作弧；以点 $C$ 为圆心，半径为 $5\ cm$ 作弧。

(iii) 将两弧的交点命名为点 $A$。

(iv) 连接 $AC$ 和 $BC$。$\Delta ABC$ 即为所求三角形。

证明

在 $\Delta ABC$ 中，我们有：

$BC= 5\ cm$，$\angle B=60^o$ 和 $\angle C=60^o$

我们知道：

三角形内角和始终等于 $180^o$

$\angle A+\angle B+\angle C = 180^o$

这意味着：

$\angle A+60^o+60^o=180^o$

$\angle A+ 120^o=180^o$

$\angle A=60^o$

我们知道：

等角对等边

因此，我们得到：

$CA=AB=5\ cm$

我们有：

$BC=CA=AB=5\ cm$ 并且

$\angle A=\angle B=\angle C=60^o$

因此，得证。

教程点

更新于: 2022年10月10日

56 次浏览

开启你的 职业生涯

完成课程获得认证

开始学习