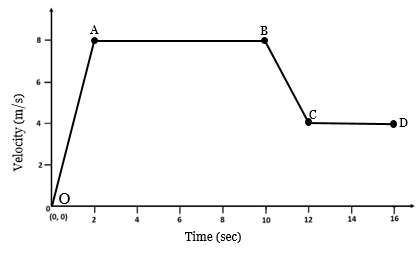
求出0-2秒、2-10秒、10-12秒、12-16秒时间段内的位移和加速度。此外，说明所有区域的运动类型。
"\n

你好，Dania，

对于这个问题，首先，我们标记点及其坐标。

 在 0−2 秒 (区域 OA)

加速度 = OA的斜率 位移 = 速度−时间(v−t) 图像下的面积

                            = x2​−x1​y2​−y1​​                                                           =  三角形AOP的面积

                            = 2−08−0                                                                                                                                                                                                                                           ddceede​

                                                                                                                            =  21​×OA×OP

                           =28​                                                                     = 21​×2×8

                       = 4 m/s2                                                              = 8 m

 In 2−10 seconds (Region AB)

斜率 = 线段AB 的 斜率                位移 = 速度 时间 图 下方 的 面积−时间(速−度) 图

                             = x2​−x1​y2​−y1​​                                                          = 矩形ABQP的面积

                             = 2−08− 8                                                    scwwcwcece                                                                                                                                                     ddceede​

                                                                                                                            =  1/2 × OA × OP

                             =20​                                                                =  8 ×8

                             = 4 m/s2                                                         = 64 m

Acceleration = Slope of BC                Displacement = Area under velocity−time(v−t) 图

                             =x2​−x1​y2​−y1​​                                                         =21​ × (平行边 之和 ) × 高  

                             =12−104−8                                                    scwwcwcece                                                                                                                                                     ddceede​

                                                                                                                            =  21​× (BQ + CR) × QR

                             =2-4​                                                                 = 21​× (4 + 8) × 2

                             =−2 m/s2                                                        =12 m

Acceleration = Slope of CD                Displacement = Area under velocity−time(v−t) 图

                             = x2​−x1​y2​−y1​​                                                          = 矩形CDSR的面积

                             =16−124−4​                                                         =21​ × Length(CD) × Breadth(CR) 

                             =40​                                                                   = ​4 × 4

                             = 0 m/s2                                                          = 16 m

OA区域运动 = 匀加速运动

AB区域运动 = 匀速运动（无加速度）

BC区域运动 = 匀减速运动

CD区域运动 = 匀速运动（无加速度）

总位移 = OA区域位移 + AB区域位移

                                            +BC区域位移  +CD区域位移

                                         = 8 + 64 + 12 + 16  

                                         =100

这里我们求的是位移而不是方向，因为这是一个速度-时间图。

要找到距离，我们应该有一个速度-时间图。